IMAGES DE FRACTALES AVEC APL2 IBM  POUR WINDOWS

Claude Chachaty

 

 

    L’importance du concept d’objet fractal, introduit dans les années soixante dix par Mandelbrot [1], provient de ce que la plupart des objets naturels ont une structure fractale alors que les objets fabriqués sont en majorité Euclidiens. Pour préciser ce concept, citons la définition qu’en donne Mandelbrot [2] : « FRACTAL . adj. Sens intuitif. Se dit d’une figure géométrique ou d’un objet naturel qui combine les caractéristiques que voici. A) Ses parties ont la même forme ou structure que le tout à ceci près qu’elles sont à une échelle différente et peuvent être légèrement déformées. B) Sa forme est, soit extrêmement irrégulière, soit extrêmement interrompue ou fragmentée, et le reste, quelle que soit l’échelle d’examen. C) Il contient des «éléments distinctifs » dont les échelles sont très variées et couvrent une très large gamme… ».

    L’ interêt scientifique et l’ aspect esthétique des fractales ont motivé la conception de nombreux algorithmes pour  les modéliser, dont on peut trouver des exemples dans [3]. Pour être satisfaisantes, ces représentations nécessitent des dizaines et parfois des centaines de milliers de points généralement calculés par des méthodes itératives. Il en résulte la saturation de la zone de travail ou un temps de calcul prohibitif en APL pour PC. Ces difficultés tendent à disparaître du fait de la progression rapide des performances des ordinateurs personnels. Reste la question du graphique pour lequel le plus répandu des tableurs, EXCEL, ne convient pas toujours. Ce problème peut être en grande partie résolu en utilisant la zone GRAPHPAK du logiciel APL2 pour WINDOWS d’IBM [1]. Trois fonctions de cette zone sont particulièrement utiles pour la représentation des fractales :

 

SPLOT : représente un tableau XY1Y2…Yn en courbes continues ou en points.

SURFACE : représente une surface F(X,Y) en perspective.

CONTOUR : projette les courbes de niveaux de F(X,Y) dans le plan XY.

 

Pour une zone de 32 Mo, la taille limite des graphiques obtenus avec ces fonctions est de l’ordre de 100000 points.

    Des courbes ou des surfaces fractales de formes très complexes, faisant l’objet d’études mathématiques sophistiquées, sont souvent obtenues à partir d’ algorithmes d’une grande simplicité; nous en donnons quelques exemples en version APL2.

 

On peut classer en deux catégories principales les fractales : les fractales déterministes ou à homothétie interne et les fractales aléatoires [3].

Les fractales déterministes sont généralement obtenus par itération d’une fonction analytique F(z) de la variable complexe  z = x + iy (x+¯11±y en APL IBM). A chaque itération on assigne à x et à y les parties réelle (Re) et imaginaire (Im) de F(z) (9±F et 11±F en APL IBM) et on utilise ces valeurs pour calculer F(z) à l’itération suivante [4, 5]

    L’exemple classique de fractale déterministe est l’ensemble de Mandelbrot de    z² + c. c est un élément d’un vecteur complexe dont la dimension détermine le nombre de points du graphique. Dans la fonction MSET, pour chaque élément indicé par j de ce vecteur, on itère le calcul de  R² = x² + y² jusqu’à ce que R² atteigne une valeur élevée, fixée arbitrairement. Le nombre d’itérations n limité à n = NMAX et porté en fonction de ReC et ImC, constitue le tableau à représenter, nommé par la suite FXY.

 

’ MSET;ŒIO;n;j;CH;x;y;z

[1]   ŒIO„1 ª CH„0

[2]   L0:'Avec potentiel ? [1]' ª eq„Œ

[3]   'Xmin Xmax :' ª (Xmin Xmax)„Œ

[4]   'Ymin Ymax' ª (Ymin Ymax)„Œ ª …(CH=1)/L1

[5]   'Nombre de points en X et en Y :' ª NPT„Œ

[6]   L1:TXY„Xmin,Xmin+((Xmax-Xmin)÷NPT-1)×¼NPT-1

[7]   TXY„,TXY°.,Ymin,Ymin+((Ymax-Ymin)÷NPT-1)×¼NPT-1

[8]   dim1„½TXY ª …(CH=1)/L2

[9]   'Nombremax d''itérations : ' ª NMAX„Œ

[10]  L2:j„1 ª POT„nit„¼0 ª t0„ŒAI[2]

[11]  L3:(cx cy)„œTXY[j] ª x2„y2„x„y„n„0

[12]  L4:n„n+1

[13]  z„x+¯11±y ª x2„x×x„cx+9±z*2 ª y2„y×y„cy+11±z*2

[14]  …((n<NMAX)^10000>x2+y2)/L4

[15]  –(eq¬1)/'dim2„½nit„nit,n'

[16]  –((eq=1)^n<NMAX)/'pot„0.5×(µx2+y2)÷2*n'

[17]  –((eq=1)^n=NMAX)/'pot„0'

[18]  –(eq=1)/'dim2„½POT„POT,pot'

[19]  …(dim1‰j„j+1)/L3

[20]  'Durée (s) : ',0.001׌AI[2]-t0

[21]  –(eq¬1)/'FXY„(2½dim2*0.5)½nit'

[22]  –(eq=1)/'FXY„(2½dim2*0.5)½POT'

[23]  L5:'Plot sections [1], surface [2], niveaux [3] ? '

[24]  –(1=srf„Œ)/'SECTIONS'

[25]  –((srf=2)/'SURF'),(srf=3)/'NIVEAUX'

[26]  L6:'Domaine complexe [1], replot [2]'

[27]  …(1 2=CH„Œ)/L0,L5

 

Les fonctions graphiques SURF et NIVEAUX sont  des adaptations des fonctions SURFACE et CONTOUR mentionnées plus haut. La fonction SECTIONS utilise SPLOT et découpe la surface FXY en éléments équidistants d’épaisseur DZ avec projection dans le plan XY des points compris entre Z et Z+DZ représentés par des symboles et des couleurs différents selon les niveaux.

 

 

Figure 1. Courbes de niveaux de l’ensemble de Mandelbrot de z² + c dans le domaine  0.33 £ ReC, ImC £ 0.39.

 

 

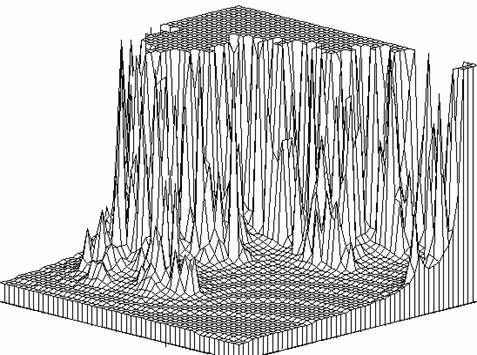
Figure 2.Ensemble de Mandelbrot de z² + c dans le domaine 0.3 £ ReC, ImC £ 0.5.

 

 

L’option eq = 1 de MSET construit  FXY avec des valeurs égales au potentiel 0.5(ln(R²))/2ⁿ pour n < NMAX et nulles pour n = NMAX.

 

 

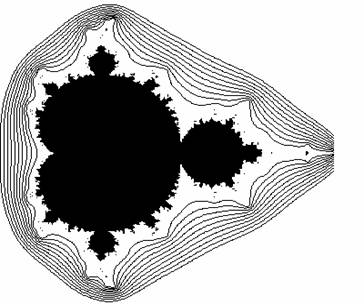
Figure 3. Représentation globale de l’ensemble de Mandelbrot de z² + c

entouré de courbes équipotentielles, par la fonction MSET avec eq = 1.

 

   Un algorithme assez semblable à celui utilisé pour MSET permet de représenter avec la fonction FONCZ les ensembles de Julia [5] de fonctions telles que lexp(z), lsin(z), lsinh(z) etc…où l est un nombre complexe.

 

’ FONCZ;ŒIO;n;j;CH;x;y;z;Z;F;R

[1]   ŒIO„1 ª CH„0 ª 'sin(Z) [1], cos(Z) [2], sinh(Z) [5]'

[2]   'cosh(Z) [6], autre fonction [0]'

[3]   –(0=F„Œ)/'''Expression de F(z) : '' ª FZ„�'

[4]   L0:'Xmin Xmax :' ª (Xmin Xmax)„Œ

[5]   'Ymin Ymax' ª (Ymin Ymax)„Œ

[6]   'Lambda (2 valeurs) : ' ª LAM„+/(1,¯11±1)׌

[7]   …(CH=1)/L1

[8]   'Nombre de points en X et en Y :' ª (NPX NPY)„Œ

[9]   TXY„Xmin,Xmin+((Xmax-Xmin)÷NPX-1)×¼NPX-1

[10]  dim1„½TXY„,TXY°.,Ymin,Ymin+((Ymax-Ymin)÷NPY-1)×¼NPY-1

[11]  'Nombremax d''iterations : ' ª NMAX„Œ

[12]  L1:j„1 ª nit„¼0 ª t0„ŒAI[2]

[13]  L2:(x y)„œTXY[j] ª n„0

[14]  L3:n„n+1 ª z„x+¯11±y

[15]  –(F¬0)/'Z„LAM×F±z' ª –(F=0)/'Z„LAM×–FZ'

[16]  (x y)„(9 11)±Z ª R„x×x ª R„R+y×y ª R„R*0.5

[17]  …((n<NMAX)^50>R)/L3 ª dim2„½nit„nit,n

[18]  …(dim1‰j„j+1)/L2 ª 'Durée (s) : ',0.001׌AI[2]-t0

[19]  FXY„(2½dim2*0.5)½nit (la suite est identique à MSET)  

 

 

 

 

 

Figure 4. Ensembles de Julia de : A) (1+0.5i)sin(z) , B) (1+0.5i)cosh(z).

 

    L’examen des  images de fractales déterministes dans le plan XY montre clairement leur propriété d’autosimilitude : chaque détail d’une image est reproduit à une échelle différente. Dans le cas de fractales aléatoires tels qu’un solide poreux ou la mousse d’un liquide, cette propriété n’a qu’un caractère statistique. La répartition spatiale des pores ou des bulles est aléatoire mais la «hiérarchie » de leurs tailles est invariante avec l’échelle d’observation sur plusieurs ordres de grandeur; elle dépend  de la dimension fractale D_f du système, dont Mandelbrot [2] donne donne la définition suivante :

« DIMENSION FRACTALE. n.f. Sens générique. Nombre qui quantifie le degré d’irrégularité et de fragmentation d’un ensemble géométrique ou d’un objet naturel et qui se réduit, dans le cas des objets de la géométrie usuelle d’Euclide, à leur dimensions usuelles. . . »

    Les courbes et les surfaces fractales ont ainsi des dimensions 1< D_f <2 et     2< D_f <3 . La notion de dimension fractale est fondamentale en physique des milieux désordonnés car elle régit les phénomènes de diffusion et d’échange (voir par exemple [6, 7]). Dans le cas de fractales de surface comme  certains adsorbants ou  catalyseurs, leur rapport surface/volume et donc leur efficacité sont d’autant plus grands que D_f  est élevé. Ce rapport tend vers l’infini lorsque D_f  approche  la limite théorique de 3.

 

    Parmi les méthodes utilisées pour représenter les courbes et les surfaces fractales aléatoires [8], la plus simple consiste à effectuer la transformée de Fourier inverse d’un vecteur ou d’un tableau de nombres complexes r₀r₁exp(ij) (r0×r1ׯ12±phi en APL IBM) où r₁ et j sont des variables aléatoires et r₀, une fonction de D_f. La fonction FRACT2D, basée sur cette méthode, est destinée à représenter les surfaces fractales.

 

’ FRACT2D;ŒIO;CH;p

[1]   ŒIO„1 ª CH„0 ª INITGAUSS

[2]   'Dimension en x et y du tableau (NP„2*entier) :'

[3]   p„p×p„¼NP„Œ

[4]   L0:'Dimension fractale 2<DF<3 : '

[5]   r0„(p°.+p)*¯0.5×4-DF„Œ ª …(CH=1)/L1

[6]   r1„(NP,NP)½GAUSSRND NP*2

[7]   phi„±2×((½,r0)?2*31)÷2*31

[8]   L1:FXY„9±IFFT2D r0×r1×(NP,NP)½¯12±phi

[9]   L2:'Nombre d''interpolations sinon 0 :'

[10]  –(0¬nint„Œ)/'INTERP2D'

[11]  L3:'Plot sections [1], surface [2], niveaux [3] ? '

[12]  –(1=srf„Œ)/'SECTIONS'

[13]  –((srf=2)/'SURF'),(srf=3)/'NIVEAUX'

[14]  L4:'Autre dimension fractale [1], interpoler [2]'

[15]  'Replot [3]' ª …(1 2 3=CH„Œ)/L0,L2,L3

 

    La fonction GAUSSRND génère du bruit gaussien à partir de paramètres contenus dans INITGAUSS, IFFT2D effectue la transformée de Fourier inverse du tableau r₀r₁exp(ij) dont on prend la partie réelle FXY.

     La surface FXY peut être  interpolée au moyen de la fonction INTERP2D. Il est possible d’effectuer plusieurs calculs en changeant la dimension fractale D_f qui n’intervient que dans r₀ et en gardant les mêmes valeurs des variables aléatoires r₁ et j. Cela permet d’évaluer l’influence de D_f sur  le relief d’une surface, sans modifier les coordonnées X et Y de ses éléments. On constate ainsi qu’en diminuant la dimension fractale d’un relief, on simule son érosion (figure 5).

    Le relief terrestre est considéré comme fractal avec en moyenne D_f  » 2.2. Il est possible de réaliser des paysages fictifs à partir d’images de synthèse de surfaces fractales déterministes ou aléatoires [1-3] obtenues par des méthodes dont font partie celles résumées dans cet article.

 

 

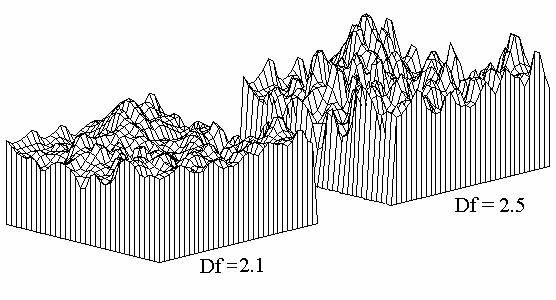
Figure 5. Influence de la dimension fractale sur le relief d’une surface. Les deux parties de l’image sont calculées avec la fonction FRACT2D pour les mêmes valeurs aléatoires de r₁ et de j.

 

 

    Ces quelques exemples montrent qu’avec un PC d’un modèle récent et sans nécessairement connaître la programmation de graphiques, il est facile d’obtenir des images satisfaisantes de fractales avec GRAPHPAK. Ces images sont loin d’atteindre le niveau artistique de celles représentées dans des ouvrages spécialisés, mais peuvent être améliorées à l’aide par exemple du programme PAINT de WINDOWS.

 

 

 

Références

 

1 - B. Mandelbrot. Les objets fractals : forme, hasard et dimension. Flammarion, Paris 1975.

 

2 - B. Mandelbrot. ibid., troisième édition suivie de Survol du langage fractal. Nouvelle Bibliothèque Scientifique, Flammarion, Paris 1989 (ISBN 2-08-211188-1).

 

3 - M.F.  Barnsley, R.L. Devaney, B.B. Mandelbrot, H.-O. Peitgen et D. Saupe.

The science of fractal images. Edité par H.O. Peitgen et D. Saupe, Springer-Verlag, Berlin, 1988 (IBSN 3-540-96608-0).

 

4 - H.-O. Peitgen dans [3] chap. 4 : Fantastic deterministic fractals.

 

5 - R.L. Devaney dans [3] chap. 3 : Fractal patterns arising in chaotic dynamical systems.   

 

6 - A. Blumen, G. Zumofen et J. Klafter. Random walks on fractals dans Structure and dynamics of molecular systems pp. 87-100, édité par R. Daudel et al., D. Reidel Publishing Company, Dordrecht 1985 (ISBN 90-277-1977-2).

 

7 - C. Chachaty, J.-P. Korb, J.R.C. van der Maarel, W. Bras et J.P. Quinn,

Fractal structure of a cross-linked polymer resin : A small-angle X-ray scattering, pulsed field gradient and paramagnetic relaxation study.

Physical Reviews B. 44, 4778-4793 (1991).

 

8 - D. Saupe dans [3] chap. 2 : Algorithms for random fractals.