Transformation de Fourier sous APL

par Henri Leblond

Introduction

Mes débuts avec l'APL remontent aux années 1975. A cette époque héroïque, il fallait un bon quart d'heure pour réussir une connexion entre Nancy, mon lieu de travail et le serveur du CEA de Saclay, puis commencer à écrire quelques lignes de code obscure sur un clavier qui l'était encore plus.

Chercheur en acoustique, j'avais essayé d'imaginer un programme permettant de traduire l'algorithme FFT de Cooley et Tukey en APL. Mais compte tenu de ma faible maîtrise du langage et du peu de souplesse des outils mis à ma disposition j'abandonnais rapidement ce projet et m'éloignais progressivement de l'APL.

J'ai repris goût, récemment, dans un cadre plus privé que professionnel, avec ce langage passionnant. La possibilité de travailler en APL sous Windows ouvre de nouveaux horizons, et la barrière des claviers exotiques a disparu. Mais avec une très grande déception, et plus de vingt années après mes premières expériences, je n'arrivais toujours pas à me procurer une traduction en APL de ce fameux algorithme de Transformation de Fourier Rapide.

Une certaine obstination et quelques week-end studieux m'ont permis d'accéder enfin à ce vieux rêve. Je me propose de vous présenter le résultat de ce petit travail, en espérant qu'il suscitera quelques commentaires, critiques et optimisations.

La Transformation de Fourier

On ne traite ici que de la Transformation de Fourier Discrète, sur un nombre 2^N d'échantillons.

Le calcul de la Transformation Discrète peut s'exprimer avec la formule suivante, qui conduit à un nombre d'opérations complexes au moins égal à N²

X(m) = x(k). exp(-j 2 p m.k / N) m=0, 1, 2, ... N-1 ( f1)

avec :

x(k) le vecteur des N échantillons à transformer

X(m) le vecteur des N coefficients complexes recherchés

L'idée permettant d'effectuer un calcul plus rapide de Transformation de Fourier semble avoir été pressenti par Gauss vers 1805 ( ref 1 )

Le célèbre algorithme de Cooley et Tukey a été mis en pratique en tant que logiciel en 1965.

Le principe de la "FFT" (Fast Fourier Transform ) consiste a remarquer que l'on peut diminuer le nombre de calculs nécessaires à l'élaboration des coefficients donnés par la formule (f1) par une factorisation astucieuse de la matrice de passage du domaine temporel au domaine fréquentiel.

La réduction du nombre de calculs est d'autant plus élevée que le nombre d'échantillons à traiter est grand.

Avec l'algorithme de Cooley Tuckey, le nombre de calculs nécessaires passe de N² à N log₂ N

soit, pour 1024 échantillons à transformer, une réduction dans un rapport supérieur à 100.

J'emprunterai à un article de Weysel Omer paru dans ELECTRONICS & WIRELESS WORD de Juin 1986 une description très visuelle de cet algorithme.

En posant

= exp(- j 2 p m.k / N)

la formule f1 peut être vue comme une opération de déphasage pur (amplitude unité du multiplicateur) de valeur

Q_p = - 2 p P/ N

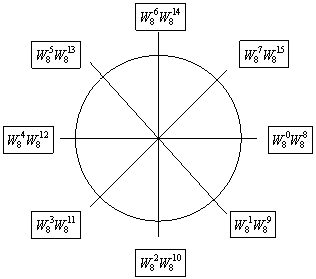
Le diagramme de Agrand montre la nature répétitive des m.k coefficients multiplicateurs complexes . Pour l'exemple présenté ci-dessous d'une transformation en 8 points, il n'y a pas 8 x 8 = 64 coefficients à calculer, mais seulement 8.

On note ainsi que

() ^p = () *

On convient ensuite de partager les éléments du vecteur des échantillons en deux suites temporelles correspondant chacune respectivement aux éléments numérotés pairs et impairs

éléments pairs de x(k) x₁(k) = x(2k)

éléments impairs de x(k) x₂(k) = x(2k + 1)

Ceci permet de réécrire la Transformation de Fourier Discrète sous la forme

X(m) = x (2k). + x (2k+1) .

Et puisque

= exp ( j 2 p / N)² = exp ( j 2 p / N /2) =

l'expression devient

X(m) = x₁(k). + x₂(k).

dans laquelle

X₁(m) est la Transformation Discrète sur N/2 points de x₁ (k)

et X₂(m) celle de x₂(k), également sur N/2 points.

Soit encore

X(m) = X₁(m) + X₂(m)

On a ainsi décomposé la séquence de N valeurs en deux demi-séquences de N/2 -1 valeurs

La séquence X(m) est définie pour 0 £ m £ N -1 alors que les séquences X₁(m) et X₂(m) sont elles définies pour 0 £ m £ N/2 -1 points.

La règle de calcul de l'équation pouvant être présentée comme suit:

X₁(m) + X₂(m) pour 0 £ m £ N/2 -1

X (m) =

X₁(m - N/2) - X₂(m - N/2) pour N/2 £ m £ N -1

On peut de nouveau illustrer cette méthode pour une transformation sur 8 échantillons.

Les valeurs à indices pairs et impairs sont tout d'abord remaniées pour obtenir les deux séries x1(m) et x2(m) qui après transformation donnent X1(m) et X2(m). Les deux demies Transformées de Fourier Discrètes sur N/2 = 4 valeurs sont calculées à l'aide des deux équations présentées ci-dessus.

Le processus est répété jusqu'à ce que la transformation résiduelle soit réduite à une transformation sur deux points. Soit log ₂ N itérations.

Exemple illustré pour une FFT en 8 points:

x(0) 0 0 0 x(0)

x(1) 0 0 4 x(4)

x(2) 0 4 2 x(2)

x(3) 0 4 6 x(6)

x(4) 4 2 1 x(1)

x(5) 4 2 5 x(5)

x(6) 4 6 3 x(3)

x(7) 4 6 7 x(7)

Pour chaque calcul "en papillon"

A X

B Y

on a

X = A + . B

Y = A - . B

Exemple:

Pour obtenir le terme T de la deuxième ligne de la deuxième colonne on calcule

T = x(1) + W₀ . x(5)

Mise en application sous APL

L'application sous APL est simple.

Le code APL a été écrit sous DYALOG

La fonction principale "fourier" fait appel a deux autres fonctions utilitaires:

la fonction "rear" pour la mise en ordre des vecteurs intermédiaires

la fonction "shuff" pour réorganiser les élements du vecteur résultat du

calcul désorganisé comme suite à l'algorithme en papillon.

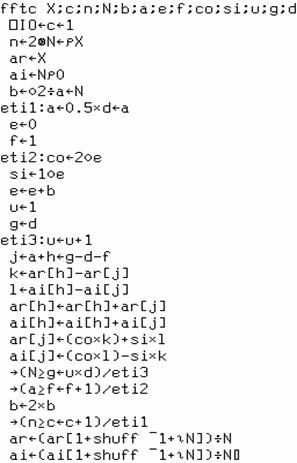
- Fonction principale "fourier"

Les lignes 1 à 8 préparent et initialisent les diverses variables intermédiaires, en particulier les deux vecteurs "sin" et "cos" correspondant respectivement aux vecteurs sinus et cosinus nécessaires à la construction du diagramme d'Agrand.

La boucle "lp" qui se déroule de la ligne 9 à la ligne 17 effectue les "log ₂ N" itérations principales, c'est à dire déroule les branches verticales du diagramme en papillon.

La boucle interne "lpj" (ligne 13 à 15) est, elle, utilisée pour réorganiser les résultats intermédiaires avant l'étape du calcul de chaque branche verticale, qui se déroule ligne 16 pour les termes réels et ligne 17 pour les termes imaginaires.

On notera que les deux calculs des termes réels et imaginaires ne peuvent être dissociés lorsqu'on utilise l'algorithme FFT.

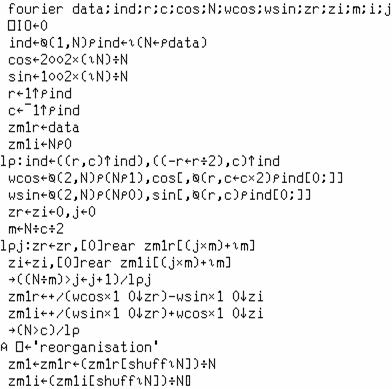
- Fonction "rear" utilisée dans la boucle "lpj":

- Fonction "shuff" pour réorganiser les données mélangées:

On réorganise les données en remarquant que l'ordre des index du résultat est l'image obtenue en renversant l'ordre des bits des index des données d'entrée exprimées en binaire:

exemple pour N = 8

index des données d'entrée	expression binaire	binaire inversé	index des données de sortie
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

soit pour la fonction shuff en APL

Résultats obtenus

La rapidité du cacul a été comparée à deux autres méthodes d'obtention d'une transformée de Fourier

1° méthode

Transformation de Fourier classique, par intégration de la formule [f1] exprimée sous sa forme vectorielle

2° méthode

Algorithme de Cooley et Tukey translaté directement depuis un code C, en APL.

Les listings correspondants à ces deux méthodes complémentaires sont joints en annexe.

Pour chaque cas on a mesuré le temps de calcul d'une transformation d'un vecteur réel en un double vecteur comprenant les deux parties réelles et imaginaires de la Transformée de Fourier.

Le temps de calcul est mesuré avec l'opérateur ŒTS. Le résultat est peu précis mais montre cependant clairement l'intérêt du code proposé.

La plateforme utilisée est un portable TOSHIBA 300CDS tournant sous Windows 95

avec 32 Moctets de RAM et une fréquence d'horloge de 166 Mhz. en mode normal.

Avec une version DYALOG 8.2, j'ai obtenu les temps de calcul suivants, exprimés en seconde

C	mode normal 166 MHz			mode lent ~80 MHz
Nombre d'echantillons	Transformée calcul classique	Transformée image d'une FFT écrite en code C	Transformée rapide telle que présentée	Transformée calcul classique	Transformée image d'une FFT écrite en code C	Transformée rapide telle que présentée
512	2	1	<1	4	1.5	1
1024	8	2	1	16	3.5	2
2048	30	5	4	61	8.5	5.5
4096	130	10	12	240	18	16

Conclusion

Ces travaux sont une étape bien modeste vers la recherche d'un moyen de calcul rapide d'une transformation de Fourier sous APL.

La méthode proposée peut sans doute être améliorée, en particulier il semble utile d'essayer de supprimer la boucle interne, assez "chronophage".

Il serait également intéressant de comparer les résultats obtenus avec d'autres partant d'une FFT écrite directement sous C, puis utilisée en APL à travers le mécanisme des DLL.

Nous serions heureux de recevoir des commentaires et ouvrir la discussion sur ce sujet.

Ref 1

Ondes et Ondelettes La sage d'un outil mathématique

par Barbara BURKE HUBBARD

Edition Pour la Science Diffusion Belin

ANNEXE

Code APL pour comparaison, 1° méthode

Transformation de Fourier classique, par intégration de la formule [f1] exprimée sous sa forme vectorielle.

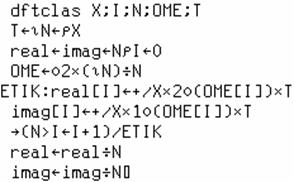
Code APL pour comparaison, 2° méthode

Algorithme de Cooley et Tukey traduit en APL, directement depuis un code écrit en C.