Le langage APL au service de la physique
Présenté à la réunion de l’AFAPL du 30
mai 2007
Claude Chachaty
claude.chachaty@wanadoo.fr
INTRODUCTION
En 1978 Gérard Langlet a donné un cours d’initiation à APL dans le laboratoire de résonance magnétique du Département de Physico-Chimie du CEA Saclay dont j’avais la responsabilité. En dépit de sérieuses limitations techniques qui n’existent plus aujourd’hui, APL a été adopté pendant plus d’une décennie comme unique langage de programmation dans ce laboratoire.
Je pratique donc APL depuis une trentaine d’années, d’abord dans le cadre de mes activités au CEA où j’ai écrit un logiciel destiné à la résonance magnétique que je continue à développer [1] et pour d’autres sujets tels que les fractales [2] et la résolution numérique des équations différentielles [3] dont nous verrons quelques applications.
J’utilise parallèlement APL2 IBM et APL+WIN. Récemment j’ai converti plusieurs worskpaces en DYALOG APL. Ces trois logiciels ont à peu près les mêmes performances pour ce qui est de la vitesse de calcul. Le mieux adapté au calcul scientifique me semble être APL2 IBM qui comporte la workspace graphique GRAPHPAK convenant bien à cette application. De plus, APL2 IBM traite un nombre complexe comme un scalaire alors qu’en APL+WIN par exemple, il est considéré comme un vecteur à deux composantes.
L’inconvénient commun à APL2 IBM et DYALOG APL est la difficulté pour les non-initiés d’utiliser le clavier APL. APL+WIN présente aussi cet inconvénient, mais à un moindre degré puisqu’un bon nombre de caractères APL peuvent être composés sur le clavier ASCII. Il est donc recommandé aux personnes utilisant mes programmes sans connaître APL. Par ailleurs APL+WIN permet d’ouvrir une fenêtre DOS pour exécuter des programmes et recueillir les résultats en APL.
Il sera question ici des applications d’APL à la géométrie fractale, aux orbites planétaires ainsi que de l’optimisation de paramètres spectroscopiques.
FRACTALES
La plupart des objets fabriqués
par l’homme relèvent de la géométrie Euclidienne alors que les objets naturels
sont de nature fractale. En géométrie Euclidienne, pour représenter une courbe,
une surface ou un volume à l’échelle R, on divise l’objet en N parties telles
que N=1/R, 1/R2 ou 1/R3. En géométrie fractale N=1/RDf. Df est la dimension fractale comprise entre 1 et 2 pour une
courbe (ex. cours de
Fractales aléatoires
Dans un fractale aléatoire, la distribution de taille des objets qui le constitue est statistiquement la même à différentes échelles. C’est le cas par exemple des bulles d’une mousse liquide. Les objets à surface fractale ont un intérêt particulier en physico-chimie car le rapport surface/volume tend vers l’infini quand la dimension fractale tend vers 3. C’est une propriété importante pour les catalyseurs de réactions chimiques et pour les résines échangeuses car on dispose d’une surface d’échange considérable dans un volume réduit. Par ailleurs, le relief des planètes rocheuses est fractal. La dimension fractale moyenne de la surface terrestre est par exemple 2.1 à 2.2.
Une surface fractale aléatoire peut être générée par une fonction telle que FRACT2D dont les éléments essentiels sont:

DF est la dimension fractale, gaussrand, une fonction qui crée du bruit gaussien avec ARAND = 231-1. IFFT2D est la fonction de transformée de Fourier inverse sur deux dimensions dont on prend la partie réelle ou imaginaire (9 ou 11○IFFT2D). Enfin -12○phi correspond à exp(i×phi).
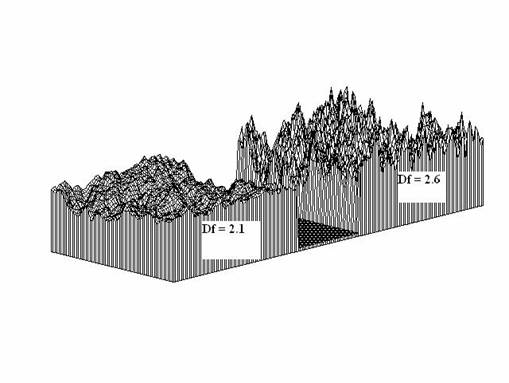
Figure 1. Surfaces fractales générées par FRACT2D. Les éléments aléatoires tels que RAU1 et phi sont les mêmes pour les deux parties de la figure qui ne diffèrent que par leur dimension fractale. Cette figure montre l’effet de cette dimension sur la rugosité d’une surface. On comprend également que l’érosion d’un massif montagneux entraîne la diminution de sa dimension fractale.

Figure 2. Topographie d’une planète fictive. Le relief tracé par MATHCAD est calculé par le programme APL EXOPLANETE comme la somme de quatre surfaces fractales dont l’une correspond à Df = 2.5 et les trois autres à Df = 2.1.
Fractales à homothétie interne
Dans le cas des fractales à homothétie interne, la forme d’un motif est reproduite exactement à différentes échelles. Il en existe de multiples exemples dans le monde végétal.
Il est remarquable que des fonctions itératives très simples comme par exemple FONCZ créent des formes extraordinairement compliquées. Cette fonction procède par les étapes suivantes :
-Calculer une fonction F(z) avec z = x+iy où x = y = ιN
-Pour chaque valeurs de x et y, prendre X = Re F(z) et Y = Im F(z)
-Itérer F(X+iY) jusqu’à ce X2+absY2
= R, R étant une valeur choisie
selon la forme de F(z)
-En chaque point du tableau {x,y}, on porte le nombre d’itérations NIT nécessaire pour atteindre R.
-L’image fractale est généralement représentée par les courbes de niveaux de NIT(x,y).

Les images fractales suivantes ont été calculées par FONCZ et tracées par MATHCAD.

Figure

Figure
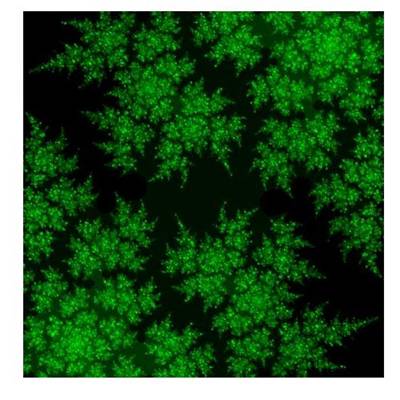
Figure
ORBITES PLANETAIRES
Le système le plus simple de l’orbite d’un satellite autour d’un astre est décrit par les équations de Newton qui admettent une solution analytique. Pour une distance initiale donnée et selon la vitesse initiale du satellite, son l’orbite est une ellipse une parabole ou une hyperbole dont un foyer est l’astre attracteur.
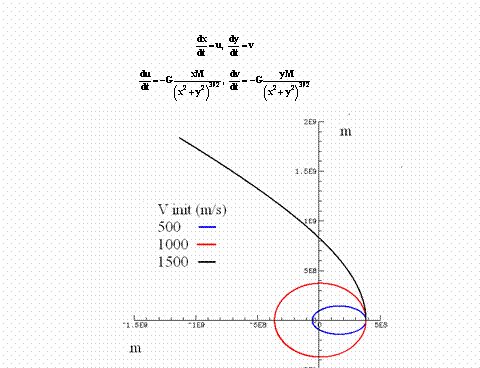
Figure 6. Orbites d’un satellite calculées avec M = 5.98×1024 kG (terre) pour les positions et vitesses initiales x = 3.85×108 m (distance moyenne terre-lune), y = 0, u = 0 et plusieurs valeurs de v. G = 6.673×10-11 m3/kG/s2 est la constante de la gravitation.
Si le satellite est soumis à l’attraction de deux astres ou plus, on ne trouve pas de solution analytique aux équations de Newton et le résultat du calcul numérique est souvent imprévisible, même en utilisant un modèle simplifié tel qu’un satellite de masse négligeable soit dans le plan orbital des deux astres dont les orbites sont des cercles centrés autour de leur centre de gravité mutuel [5].
Dans ce cas particulier le calcul de la trajectoire du satellite est effectué par le programme A3CORPS qui résout numériquement un système de quatre équations différentielles par la méthode de Runge-Kutta. Le calcul est effectué en coordonnées réduites et l’échelle de temps est la période de rotation de l’axe x qui joint les deux astres.
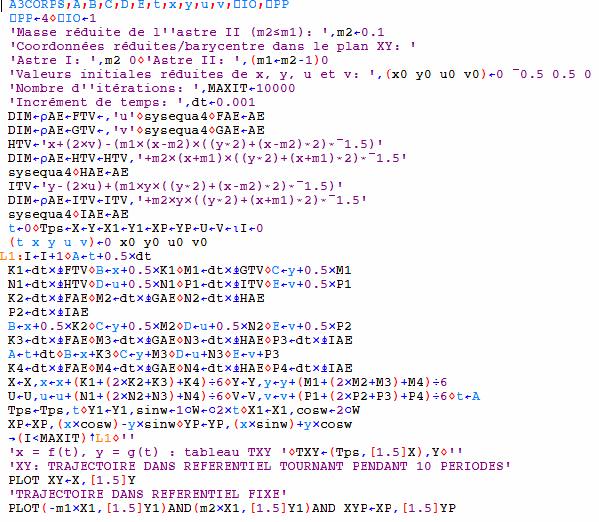
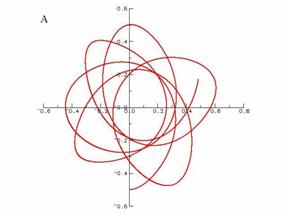
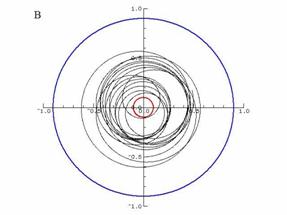
Figure 7. Trajectoires d’un corps de masse négligeable dans le champ gravitationnel de deux astres de masses réduites 0.1 et 0.9 calculées par le programme A3CORPS pour dix périodes de rotation de l’axe joignant les deux astres. A : référentiel tournant, B : référentiel fixe.
Une série de programmes basés sur un algorithme de Chaitin [6] permet de traiter le problème à N corps dans toute sa généralité. Cet algorithme utilisé par exemple dans le programme NEWTON2 qui ne concerne que deux astres, peut être facilement étendu à des systèmes plus compliqués comme on le verra plus loin.

Exemple de système à trois corps : le système soleil, terre, lune.
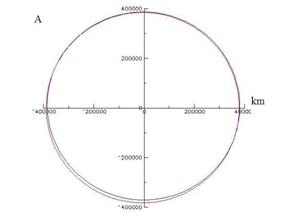
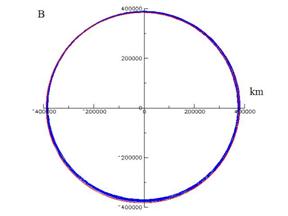
Figure 8. Orbite de la lune autour de la terre. En
rouge : orbite non perturbée, en bleu : orbite perturbée par le
soleil. A : pendant 1 période lunaire (27.3 jours), B : pendant 1 an.
Exemple de système à cinq corps : soleil, jupiter, saturne, uranus et neptune.
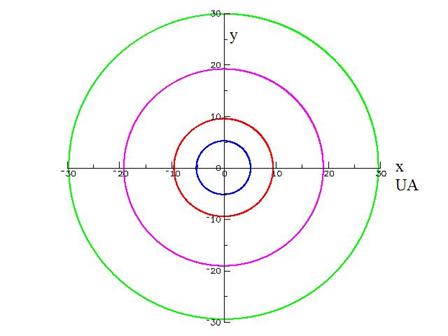
Figure 9. Orbites des planètes géantes calculées par le programme NEWTON5 en tenant compte de toutes les interactions gravitationnelles. UA : unité astronomique, distance moyenne de la terre au soleil soit 1.5×108 km.
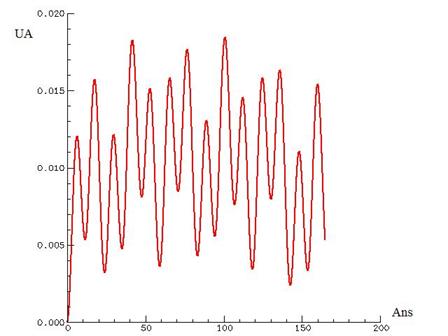
Figure 10. Déplacement radial du soleil (selon Y) sous l’influence des 4 planètes géantes pendant une période de révolution de neptune autour du soleil (164.65 ans). L’influence des planètes telluriques est négligeable. La mesure d’un tel déplacement a permis la première détection d’une planète extra-solaire en 1995 par Mayor et Queloz de l’Observatoire de Genève. Les raies spectrales de l’étoile se déplacent vers les petites ou grandes longueurs d’onde selon qu’elle se rapproche ou s’éloigne de l’observateur (effet Doppler).
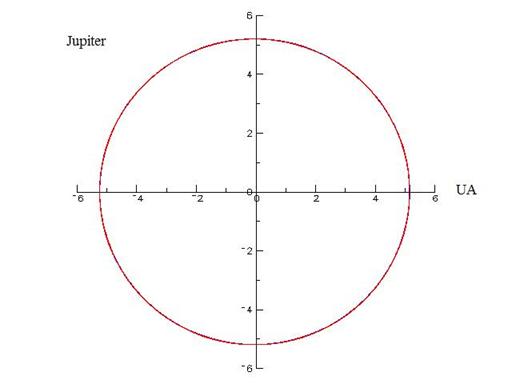
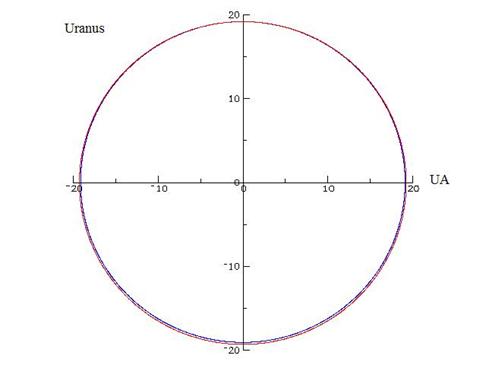
Figure 11. Orbites de jupiter et d’uranus perturbées
(bleu) et non perturbées (rouge) par les autres planètes. Pour jupiter, beaucoup plus proche du soleil qu’uranus, la différence entre les deux types d’orbites est
imperceptible sur cette figure. Neptune se comporte à peu près comme uranus.
Dans le cas de saturne, la perturbation est visible mais moins nette que pour
ces deux planètes.
En 1846 Le Verrier et Adams annoncèrent parallèlement que les perturbations observées dans l’orbite d’Uranus étaient dues à une planète inconnue jusqu’alors, neptune, qui fut observée par Galle la même année. Pour évaluer ces perturbations on calcule l’orbite d’uranus par le programme NEWTON5 mentionné plus haut, avec et sans neptune.
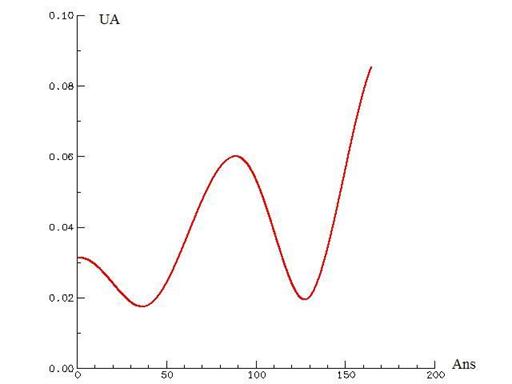
Figure 12. Influence de neptune
sur le mouvement orbital d’uranus (écart entre
l’orbite perturbée et non perturbée) durant une révolution de neptune autour du soleil. La perturbation moyenne sur cette
période est de 0.0385 UA.
OPTIMISATION
DE PARAMETRES
Pour
extraire les valeurs des paramètres d’une courbe expérimentale Y=F(x,P) on ajuste par
les moindres carrés à cette courbe, une courbe calculée Z=G(x,p) simulant la courbe Y sur la base
d’une théorie appropriée et avec des paramètres initiaux vraisemblables.
Les
vecteurs p et P sont respectivement les valeurs approximatives et les valeurs expérimentales
des paramètres. Pour obtenir les valeurs de P recherchées, il est commode de multiplier p par un vecteur B dont
les composantes initiales B1 sont égales
à 1.
L’optimisation de B est effectuée par la fonction B←Y MARQ B1 qui minimise (Y-Z←G B)*2. La fonction MARQ est une version améliorée par M.A. Jenkins, de l’algorithme de Levenberg-Marquardt [7]. Elle a le mérite d’être assez peu sensible au choix des paramètres initiaux du moment que leurs ordres de grandeur sont respectés.

Application.
Dans les membranes biologiques, le cholestérol ne se répartit pas d’une manière homogène. Pour connaître la proportion des domaines enrichis ou appauvris en cholestérol ainsi que certaines de leurs propriétés physiques telles que l’ordre moléculaire et la fluidité, l’une des méthodes que l’on utilise est la résonance paramagnétique électronique (RPE).
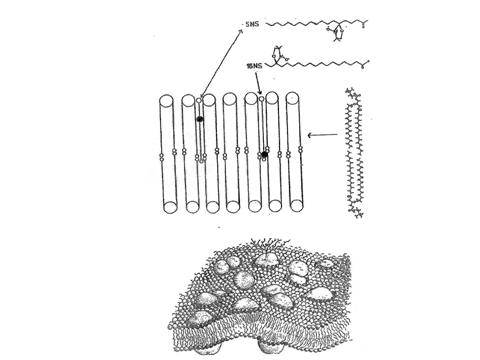
Figure 13. Représentation schématique des doubles couches d’une membrane de phospholipides dans laquelle on insère une sonde d’acide stéarique marqué par un groupe radicalaire ● dont on enregistre le spectre RPE. Selon la position de ce groupe, on peut tester certaines propriétés des doubles couches (polarité, ordre moléculaire, fluidité) pour différentes profondeurs d’immersion de la sonde. La partie inférieure de cette figure est une représentation plus réaliste d’une telle membrane avec des inclusions de protéines.
Les membranes sont des cristaux liquides lamellaires dans lesquelles les molécules tendent à s’orienter autour d’une direction privilégiée, le directeur, perpendiculaire à la surface d’une double couche. Pour un cristal liquide lamellaire, l’amplitude de libration des molécules autour du directeur est caractérisée par un paramètre d’ordre S compris entre 0 et 1. Ces deux limites correspondent respectivement à l’état liquide isotrope (liquide ordinaire) et à l’état solide.
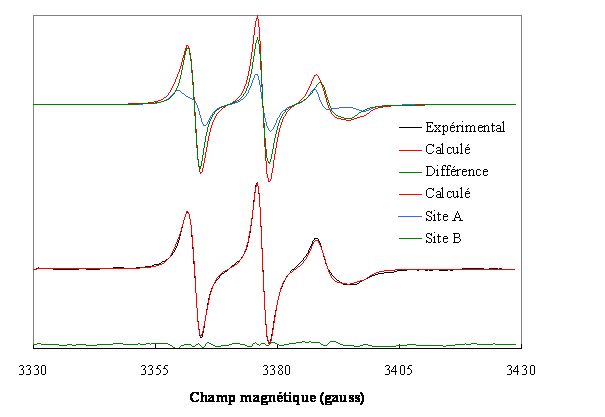
Figure 14. Spectre RPE d’une sonde radicalaire dans une membrane contenant du cholestérol. La dérivée d’absorption du rayonnement micro-onde est tracée en fonction du champ magnétique appliqué. Le diagramme inférieur comporte le spectre expérimental, le spectre simulé après optimisation des paramètres et leur différence. Le diagramme supérieur indique que le spectre simulé est la somme de deux spectres correspondant respectivement aux domaines enrichis en cholestérol, les mieux ordonnés (site A, 38%, S = 0.279) et aux domaines désordonnés (site B, 62%, S = 0.141) dépourvus de cholestérol. Le principe de ces simulations est exposé dans la réf. [1].
REFERENCES
1a - C. Chachaty, APL, a Powerful Research Tool in
Magnetic Resonance Spectroscopy.
APL Quote
Quad, 34 (4), 69 (2002). APL2002,
Madrid 22-25 Juillet 2002.
1b – C. Chachaty, Analysis and
Simulation of Electron Spin Resonance Spectra of Randomly Oriented Paramagnetic
Species. Site www.esr-spectsim-softw.fr
2 - C. Chachaty, Images de
fractales avec APL2 IBM pour Windows. Les Nouvelles d'APL, 31, 29 (1999).
3 - C. Chachaty, Quelques
fonctions APL simples pour la résolution numérique des équations et systèmes
différentiels. Les Nouvelles d'APL, 27,
61 (1998).
4
- R.F. Voss, Fractals
in nature: from characterization to simulation. Dans “The Science of Fractal Images”,
H.O.Peitgen, D. Saupe éditeurs,
5 - P. Hellings, “Astrophysics with a PC: an introduction to
computational astrophysics”,1994, William Bell,
Richmond (USA), ISBN 943396-43-3.
6 - G.J. Chaitin, An APL2 Gallery of
Mathematical Physics- A Course Outline.
Proceedings Japan 85 APL Symposium, N:GE18-9948-0, IBM Japan, pp1-56.
7 - D.W.
Marquardt, J.
Soc. Ind. Appl. Math. 11, 431 (1963).