TRANSFORMEES
INVERSES DE LAPLACE DES FRACTIONS RATIONNELLES
par Charles Hubert
La
transformation de Laplace
A
une fonction du temps f(t) nulle pour t<0, la transformation de Laplace fait
correspondre une fonction F(p) d'une variable complexe p. La transformation et
son inverse sont exprimées par les relations
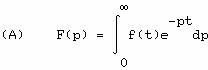
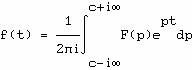
Dans
(A.2) le chemin d'intégration est une droite et c doit être supérieur aux
parties réelles de toutes les singularités de F(p) ce qui entraîne f(t)=0 pour
t<0 ; l'intégrale (A.1) est définie pour Re(p)>c et la fonction
obtenue s'étend pour Re(p)≤c par prolongement analytique. Dans la suite
on utilisera une minuscule pour chaque fonction de t et la majuscule
correspondante pour sa transformée de Laplace.
Cette
transformation est linéaire :
Elle
transforme la dérivation par rapport à t en multiplication :
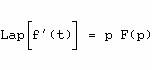
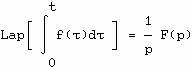
Les équations différentielles sont alors transformées en équations algébriques.
Exemples :
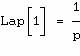
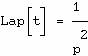
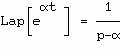
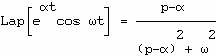
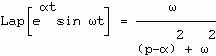
Un
système dynamique possède en général une ou plusieurs entrées et une ou
plusieurs sorties. Par exemple dans un avion, le braquage de la gouverne de
profondeur est une entrée et l'altitude est une sortie ; ces grandeurs et
d'autres sont reliées par les équations de la mécanique du vol.
La
transformation de Laplace s'applique aux systèmes dynamiques invariants (les
fonctions du temps ne figurent dans les équations qu'aux entrées) et linéaires.
Un tel système étant initialement au repos (tout à zéro), si on applique à une
entrée un signal e(t) dont la transformée de Laplace est E(p) et si S(p) est la
transformée de Laplace du signal s(t) qui en résulte à une sortie, on démontre
qu'il existe une fonction T(p) indépendante de E(p) telle que
cette fonction T(p) est la fonction de transfert de l'entrée vers la sortie
considérées. Une simple multiplication de fonctions donne la transformée de
Laplace de la réponse à un signal donné.
Si
le système obéit à un système différentiel linéaire à coefficients constants,
cette fonction de transfert T(p) est une fraction rationnelle. Si de plus E(p)
est aussi une fraction rationnelle, ce qui est fréquent au cours de l'étude de
ces systèmes, alors S(p) est aussi une fraction rationnelle ; sa
transformée inverse s(t) est la réponse en fonction du temps. L'intérêt du
calcul pratique de la transformée inverse d'une fraction rationnelle en
résulte.
Et
la transformation de Fourier ?
Faisons
ici une remarque. Il existe un parenté entre les transformations de Laplace et
de Fourier mais leurs domaines d'application sont différents. La transformation
de Fourier et son inverse peuvent être décrites en posant p=ωi dans les
formules (A), en intégrant de 
dans (A.1) et en prenant c=0 dans (A.2).
La
transformation de Fourier s'applique à des fonctions f(t) pouvant être
différentes de zéro aussi bien pour t<0 que pour t>0. Elle
s'applique quand une cause peut produire des effets dans les deux directions,
qui tendent vers zéro à l'infini ; t est une variable d'espace.
La
transformation de Laplace s'applique à des fonctions f(t) nulles
pour t<0. Elle s'applique quand une cause ne peut produire des effets
que dans une seule direction, qui ne tendent pas forcément vers zéro quand t
tend vers 
;
t est le temps et une cause n'a aucun effet vers le passé.
Calcul
de la transformée inverse d'une fraction rationnelle
Considérons
par exemple un système dont la fonction de transfert est
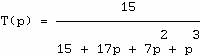
On
lui applique un échelon d'amplitude 2 : à l'instant 0 l'entrée
passe de la constante 0 à la constante 2. On déduit d'un exemple précédent
que sa transformée de Laplace est E(p) = 2/p. La transformée de
Laplace de la sortie est donc
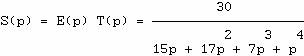
Pour
calculer numériquement la transformée inverse s(t), il faut représenter
cette fraction sous la forme d'une matrice à deux lignes : numérateur puis
dénominateur. On représente le polynôme de chaque ligne par tous ses
coefficients, zéros compris, suivant les puissances croissantes. Il faut donc
que S soit sous la forme
qu'on peut générer par l'expression APL
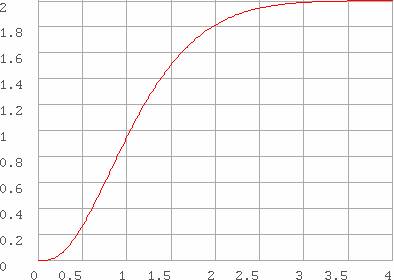
La
transformée inverse de s(t) pour 
subdivisé en 200 intervalles égaux
s'obtient par l'expression
si on veut que le résultat soit affecté à une variable s. Ce résultat a la
forme d'une matrice à deux colonnes : les valeurs de t dans s[;0],
puis celles de s(t) correspondantes dans s[;1]. Vérification avec
l'expression analytique (en origine 0) :
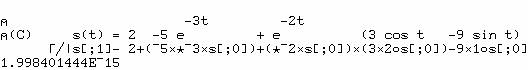
qui est ainsi le maximum des valeurs absolues des différences entre les valeurs
de s(t) calculées par FntLap et celles calculées par l'expression qui développe
la formule analytique.
L'une
des bornes de l'intervalle temporel n'est pas obligatoirement zéro ; on
peut calculer
ou encore
si l'on veut. Quand zéro fait partie de l'intervalle temporel, il figure deux
fois dans le résultat, pour 0-ε et 0+ε, afin de rendre compte de
la discontinuité éventuelle de la transformée inverse. Autre exemple :
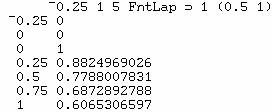
et puisque
on peut vérifier :
Bien
entendu les arguments droit et gauche de FntLap peuvent résulter d'expressions
calculées, et le résultat de FntLap, au lieu d'être affecté à une variable,
peut servir d'argument à une fonction :
par exemple, si 0 Plot construit le graphe de s(t) et si Graf l'affiche à
l'écran.
L'argument
peut ne contenir qu'une valeur ; alors FntLap donne la matrice
correspondant à cette valeur de t :
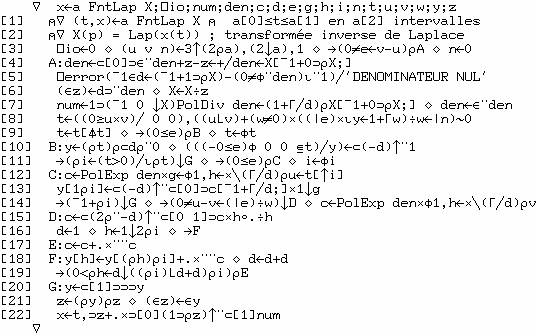
La
fonction FntLap ne se limite pas à inverser une seule transformée de
Laplace ; elle se généralise de deux façons.
1)
FntLap permet de calculer en même temps les transformées inverses de plusieurs
fractions qui ont le même dénominateur. Dans un système invariant linéaire
ayant plusieurs entrées et‑ou plusieurs sorties, il y a plusieurs
fonctions de transfert ; celles-ci ont le même dénominateur et cette
généralisation de FntLap s'y applique. Le dénominateur commun doit se trouver
dans la dernière ligne de l'argument droit et les numérateurs dans les autres
lignes. Exemple avec deux numérateurs :
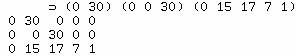
si bien que
calcule en même temps les transformées inverses de
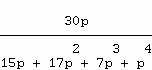
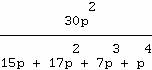
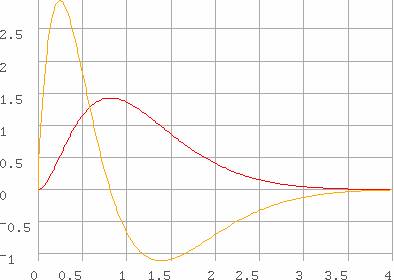
et place les résultats dans s, matrice à trois colonnes : le
temps t puis les deux transformées inverses s'(t)
et s"(t) ; le nombre de colonnes de s est égal au nombre de
lignes de l'argument droit. Vérification avec les expressions analytiques :
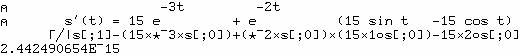
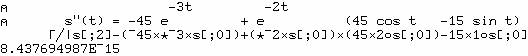
2)
FntLap accepte dans l'argument droit une matrice gigogne à condition que les
tableaux contenus dans les cases de cette matrice correspondant à une même
fraction rationnelle aient des structures compatibles. FntLap calcule en même
temps les transformées inverses des fractions dont les coefficients ont les
valeurs contenues dans les cases correspondantes. Cela permet d'étudier
l'influence sur la réponse de la variation des paramètres d'un système. Par
exemple l'argument droit de
décrit une fraction dont le numérateur prend trois valeurs et dont le
dénominateur prend trois valeurs aux degrés 1 et 2 et une valeur aux
degrés 0, 3 et 4 ; cela correspond aux trois fractions
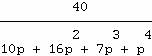
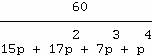
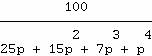
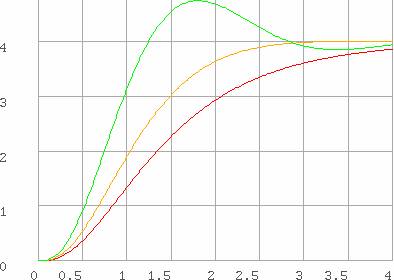
Après
exécution s est une matrice à deux colonnes : t et s(t) ;
chaque case de la colonne s(t) contient un vecteur à trois composantes, c'est
la dimension résultant des dimensions compatibles des cases de l'argument
droit. Vérification avec les expressions analytiques :
pour
la fraction 40/... :
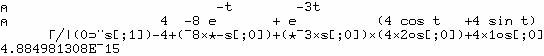
pour
la fraction 60/... :
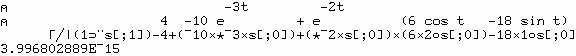
pour
la fraction 100/... :
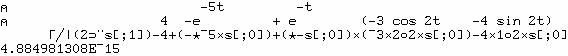
Les
méthodes rejetées
Voyons
les méthodes de calcul déconseillées et qu'on n'a donc pas programmées dans
FntLap.
1)
Pour calculer à la main l'expression analytique, pour t>0, de la transformée
inverse de Laplace d'une fraction rationnelle F(p) la méthode la plus simple
consiste à faire la somme des résidus de 
pour tous ses pôles c'est-à-dire les racines
de son dénominateur. C'est toujours une combinaison linéaire de fonctions
exponentielles-circulaires déterminées par les pôles, chaque coefficient est un
polynôme dont le nombre de termes (degré moins un) est l'ordre du pôle
correspondant. Par exemple les pôles de la fraction (B) sont
0, -3, -2+i, -2-i et nous avons vu dans les vérifications que sa
transformée inverse (C) est une combinaison linéaire de 
Informatiquement, il faut calculer les racines
du dénominateur ; cela se révèle difficile en cas de racines multiples ou
presque multiples, et dans ce dernier cas le calcul est amené à faire la
différence de grands nombres, ce qui détériore la précision du résultat. De
plus pour t proche de zéro, si c'est le but d'un calcul pratique, la précision
est généralement dégradée ; on peut le voir sur l'exemple précédent, la
formule
calcule numériquement
et les valeurs 2, 5, 1, 3 font perdre des bits significatifs
utiles pour le résultat. Informatiquement l'expression (C) ne permet pas de
trouver pour 
que
2)
En effectuant indéfiniment la division du numérateur de la fraction (B) par son
dénominateur suivant les puissances croissantes de 1/p et en appliquant à
chaque terme de la série obtenue la formule
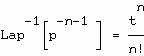
on obtient d'abord le développement en série de la fraction du même
exemple :
puis, terme à terme, celui de sa transformée inverse
On
démontre que cette méthode est mathématiquement valable pour n'importe quelle
fraction. On ne calcule pas les racines du dénominateur et on ne rencontre
aucune difficulté due à leurs particularités. La méthode est précise au
voisinage de zéro mais elle nécessite d'autant plus de termes que t est plus grand.
Si t est grand la précision peut se dégrader parce que des termes de signes
différents et de grandes valeurs absolues font perdre des bits significatifs
utiles pour le résultat.
On
peut le voir sur l'exemple simple
qui donne
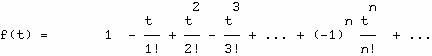
ce qui développe 
bien entendu.
Pour
t=15 par exemple il faut prendre 62 termes dont le plus grand vaut
La
somme et la bonne valeur sont
L'erreur
relative
est loin de la précision qu'on pourrait attendre de l'ordinateur.
L'erreur relative de FntLap est
3)
Toujours à propos du même exemple considérons la solution du système
différentiel
w' = x
x' = y y' = z z' = - 7z - 17y - 15x
avec les conditions initiales
w(0) = 0
x(0) = 0 y(0) = 0 z(0) = 1
La transformée inverse de (B) est alors
s = 30w
On
peut appliquer à ce système différentiel une méthode numérique d'intégration.
Ici aussi on ne se soucie pas des racines du dénominateur, mais on ne profite
ni de l'invariance ni de la linéarité du système. La précision obtenue, plus
grossière que celle de l'arithmétique de l'ordinateur, et éventuellement la
convergence du calcul dépendent du pas d'intégration et de la méthode
choisie ; et quelle méthode choisir ? Cela dépendra généralement de
la position des pôles dans le plan complexe.
La
méthode choisie pour FntLap
Cette
méthode commence par diviser les numérateurs et le dénominateur par le
coefficient de la plus haute puissance de celui-ci pour que ce coefficient
devienne égal à 1. On peut examiner la suite sur le même exemple non limitatif.
Le système différentiel explicité dans la troisième méthode précédente peut
être mis sous la forme matricielle
X' = A X
avec
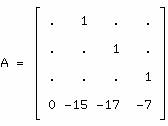
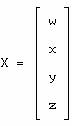
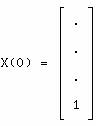
les zéros par principe ont été notés ici par des points ; A est souvent
appelée la matrice compagne du dénominateur.
Toute
solution de ce système vérifie la relation
FntLap
doit calculer
X(τ), X(τ+θ), ...
X(τ+kθ), ... X(τ+nθ)
Notons que les matrices de la forme exp(θA) pour toutes les valeurs de
θ commutent entre elles.
Pour
calculer X(τ+kθ) avec 
FntLap calcule d'abord exp(τA) et
E=exp(θA). Alors
X(τ) = exp(τA) X(0) = la dernière
colonne de exp(τA)
Par
élévations au carré successives FntLap calcule 
ce qui donne exp(2θA), exp(4θA),
exp(8θA), ...
Par simple multiplication matricielle 
permet un décalage temporel kθ. Par
multiplications successives FntLap déduit de proche en proche les
X(τ+kθ) :
Pour
une raison de programmation, FntLap travaille avec les transposées des matrices
ci-dessus. A la fin de FntLap la transformée inverse est calculée par
combinaison linéaire des composantes des X(τ+kθ), les coefficients
étant tirés du numérateur de la transformée directe (l'argument droit).
Le
calcul de exp(τA) et exp(θA) n'est pas fait en diagonalisant A car
cela ramènerait au calcul des racines du dénominateur avec les difficultés
signalées dans la première méthode précédente ; de plus en cas de racine
multiple A n'est jamais diagonalisable. Ce calcul est assuré par une fonction
PolExp (exponentielle de polynôme) parce qu'elle est appelée deux fois (τ
et θ) dans FntLap et appelée aussi par d'autres fonctions. PolExp ne
travaille pas sur la matrice τA elle-même mais profite de la structure
polynômiale du dénominateur. Disons sommairement que PolExp procède par calcul
d'un nombre suffisant de puissances successives de x=τp modulo le
dénominateur D(x) et leur applique le développement en série de l'exponentielle
limité aux puissances utiles.
Pour
que le nombre de termes ne soit pas trop grand, PolExp calcule un majorant des
modules de toutes les racines de D(x) par une méthode très simple et divise x
par une puissance entière de 2, disons 
, afin
que toutes les racines du polynôme ainsi modifié aient un module inférieur à
log 2 ; l'exponentielle obtenue est ensuite soumise à
m élévations au carré successives afin d'obtenir l'exponentielle cherchée.
Pour
que des bits utiles ne soient pas perdus dans le calcul de l'exponentielle, on
décompose chaque nombre en deux parties : le multiple entier de 1/16 le
plus proche y0 et le reste y1, de manière que y = y0 + y1 ;
alors y0 est représenté sans arrondi dans l'ordinateur. En fin de calcul
seulement les deux parties de chaque nombre sont additionnées pour donner le
nombre sous la forme habituelle. Pour voir l'utilité de cette décomposition on
peut considérer le dénominateur
dont les racines ‑1 et 
(à la précision de l'ordinateur) sont
fortement disproportionnées. Si on rapporte la matrice A à ses directions
propres, on voit que cela implique le calcul de exp(-τ) et 
. Si
τ=0.01 par exemple il faut trouver exp(‑0.01)=0.9900498337 et 
Mais à cause de 
il faut diviser τ par avec m=61 ce qui entraîne 
qui serait représenté par 1 exactement dans un
seul nombre et 61 élévations au carré donneraient 1 au lieu de 0.9900498337. La
représentation choisie place 1 et 
dans deux nombres distincts, les 61 élévations
au carré donnent 1 et ‑0.009950166251 séparément et leur somme donne bien
0.9900498337. On peut essayer
et vérifier
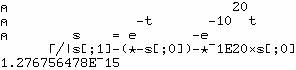
Puisque
cette méthode ne calcule pas les racines du dénominateur, elle n'est pas
sensible à leurs particularités. Elle profite de l'invariance et de la
linéarité grâce aux matrices.
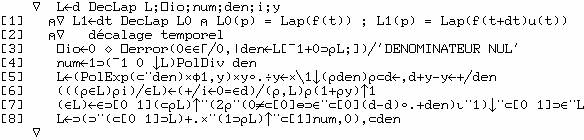
Décalage
temporel
La
transformée de Laplace F(p) d'une fonction f(t) et une durée Δt étant
données, définissons la fonction
g(t) = f(t+Δt)u(t) où
u(t) = (t>0)
qui se déduit de f(t) en décalant l'origine du temps en Δt et en annulant
la fonction avant cette nouvelle origine. Sa transformée de Laplace G(p) se
calcule ainsi
Vérification
sur un exemple :
et puisque pour g le début de l'intervalle est 0, donc répété :
La
fonction DecLap admet un argument droit de même structure que FntLap. Le
nombre de cases de l'argument gauche doit être ou un ou le nombre de numérateurs ;
le contenu de chaque case doit être compatible avec les cases des fractions
rationnelles correspondantes.
Le
décalage deltat peut être négatif, DecLap peut ainsi remonter dans le
passé :
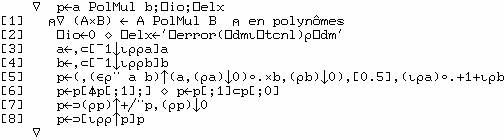
Multiplication
de polynômes
La
fonction PolMul effectue la multiplication du polynôme gauche par le polynôme
droit :
Exemple :
réalise
Cette
fonction n'est appelée ni par FntLap ni par DecLap, mais elle est souvent utile
dans les travaux où ces deux fonctions sont nécessaires.
Les
arguments ne sont pas restreints à des vecteurs. Ils peuvent être des tableaux
de rang plus élevé : la dernière dimension développe les coefficients de
chaque polynôme, les autres dimensions décrivent une liste de polynômes. Ainsi
un tableau de dimension 5 9 7 décrit une matrice à 5 lignes et
9 colonnes de polynômes à 7 coefficients. Les dimensions des
polynômes (privées des nombres de coefficients) des deux arguments doivent être
compatibles ; par exemple un tableau de dimension 5 9 7 est
compatible avec un tableau de dimension 6 : ce sont une matrice de
dimension 5 9 et un scalaire qui contiennent des polynômes et PolMul
donnera un produit de dimension 5 9 12
(degré 6 + 5 = 11).
De
plus les arguments peuvent être gigognes à la condition que les structures des
cases des polynômes à multiplier soient compatibles.
La
fonction calcule tous les produits des coefficients d'un argument par ceux de
l'autre, et en même temps les degrés de ces produits. Elle rassemble ensuite
les produits d'un même degré et en fait la somme.
Division
de polynômes
La
fonction PolDiv effectue la division du polynôme gauche par le polynôme droit
suivant les puissances décroissantes et fournit le quotient et le reste dans
les deux cases d'un vecteur de dimension 2 :
Exemple :
En
multipliant le dénominateur par le quotient et en ajoutant le reste on retrouve
bien le numérateur :
Les
arguments ne sont pas restreints à des vecteurs. Ils peuvent être des tableaux
de rang plus élevé : la dernière dimension développe les coefficients de
chaque polynôme, les autres dimensions décrivent une liste de polynômes. Ainsi
un tableau de dimension 5 9 14 décrit une matrice à 5 lignes et
9 colonnes de polynômes à 14 coefficients. Les arguments doivent être
compatibles ; par exemple un tableau de dimension 5 9 12 est
compatible avec un tableau de dimension 6 : ce sont une matrice de
dimension 5 9 et un scalaire qui contiennent des polynômes et PolDiv
donnera un quotient de dimension 5 9 7 (degrés 11 ‑ 5 = 6)
et un reste de dimension 5 9 5 (degrés 5 ‑ 1 = 4).
De
plus les arguments peuvent être gigognes à la condition que les structures des
cases des polynômes à diviser soient compatibles.
La
fonction procède par itération comme on ferait manuellement.
Calcul
sur un tableau gigogne
Pour
pouvoir traiter un tableau gigogne, FntLap développe tous les dénominateurs
décrits par l'argument droit afin de les traiter en toute sécurité.
L'expression
affecte à z un scalaire contenant un tableau de structure compatible avec
toutes les cases du dénominateur, en déduit un tableau nul de même structure,
répercute cette structure à toutes les cases du dénominateur, puis affecte à
den la liste de tous les dénominateurs distincts. L'indice du dernier
coefficient non nul de chaque dénominateur donne son degré ; les degrés
sont placés dans d et les coefficients correspondants dans z. En divisant
la fraction X par ces coefficients on ramène ceux-ci à 1. Pour supprimer
les termes impulsionnels (les parties entières) la fonction PolDiv calcule le
reste de la division des numérateurs par les dénominateurs.
La
suite de FntLap calcule exp(τA) et exp(θA) par PolExp puis les
exp(τ+kθ) définis précédemment qu'elle place dans y.
La
fin de FntLap réarrange dans z avec la bonne structure les exp(τ+kθ)
contenus dans y, puis calcule les transformées inverses en multipliant par
la matrice des numérateurs et achève en caténant une colonne de t.
La
programmation de DecLap, PolMul et PolDiv utilise les mêmes recettes que FntLap
pour gérer la structure des données.
Les
fonctions
On
peut les trouver dans le fichier APL*PLUS 'laplace.sf' ; la
composante 1 contient la table des matières, les autres composantes
contiennent les 
de ces fonctions.
