APL contre MATLAB

 

Charles HUBERT

 

Introduction

 

Dans cet article je compare les deux langages de programmation APL et MATLAB. Il existe entre eux de nombreuses différences qui influent beaucoup sur leur efficacité pratique ; mais pour ne pas lasser le lecteur je me suis limité à un petit nombre de ces différences permettant de se faire une idée.

Si MATLAB n'utilise guère que les caractères ASCII, au contraire APL se sert de caractères spéciaux (souvent des idéogrammes) plus faciles à retenir que les nombreux symboles de fonctions ou les mots réservés de MATLAB.

Dans la suite, les exemples dans les deux langages seront repérés par

MATLAB  et  APL

Si certaines fonctions de ma composition interviennent, ces repères deviendront

MATLAB/HUB  et  APL/HUB

Souvent apparaîtront côte à côte une même fonction en MATLAB et en APL afin de les comparer.

Les réponses de MATLAB sont souvent bavardes ; celles d'APL ne contiennent que l'essentiel ou que les détails qu'on a demandés. La manipulation de la zone de travail (workspace) est beaucoup plus facile en APL qu'en MATLAB.

Les symboles

 

Les deux langages contiennent des fonctions que nous appellerons primitives parce qu'ils les connaissent sans avoir à les définir : par exemple l'addition "+".

En MATLAB les primitives qui ne sont pas représentées par un ou plusieurs caractères spéciaux le sont par des symboles construits de la même façon que les symboles créés par le programmeur (exemple "size"). Celui-ci ne peut pas utiliser ces symboles, ni les mots réservés (exemple "if"), pour autre chose.

En APL une fonction ou une variable primitive est représentée, ou bien par un caractère spécial (exemple : multiplication ), ou bien par un mot préfixé par le caractère spécial  (quad, exemple : date et heure  = time stamp). Le nom d'une fonction ou d'une variable primitive contient toujours un caractère spécial ce qui empêche tout conflit avec un objet créé par le programmeur. Il n'y a pas de mot réservé.

Pendant un travail en MATLAB, une fonction "truc" (par exemple) est un fichier du même nom "truc.m" sur le disque dur. Comme c'est le nom du fichier qui compte, la fonction pourra être appelée par "TRUC" ou "Truc" ou "tRuC",... car la gestion des fichiers confond les majuscules et les minuscules ; de plus si on a remplacé "truc" par "machin" dans la ligne "function" du fichier "truc.m", MATLAB considérera qu'il s'agit toujours de la fonction "truc" et non de la fonction "machin".

Pendant un travail en APL, une fonction "truc" (par exemple) se trouve en mémoire vive (RAM). Alors "truc" ou "TRUC" ou "Truc" ou "tRuC" sont autant de fonctions différentes car APL distingue les majuscules et les minuscules. On peut en profiter pour placer une majuscule au premier caractère de chacun des mots qui composent un symbole, ce qui améliore la lisibilité ; par exemple "RacPol" signifie Racines de Polynômes.

En MATLAB, les variables se placent à deux niveaux : local (privé) et global (public). Une variable globale est accessible partout où elle figure dans une déclaration "global". Si elle ne figure pas dans une déclaration "global", elle n'est accessible que dans la fonction où elle est affectée. La déclaration "global" équivaut à la déclaration "common" du fortran.

En APL, les variables et fonctions se placent dans une arborescence dynamique. On déclare les symboles (variables et fonctions) locaux à une fonction ("Fonc" par exemple) dans sa ligne de définition. Les objets désignés par ces symboles sont accessibles dans "Fonc" et dans toute autre fonction que "Fonc" appelle directement ou indirectement, qui les traite alors comme globaux. Ces objets sont inaccessibles avant d'entrer dans "Fonc" ou après en être sorti. Cette organisation arborescente des symboles rend de grands services en APL. En MATLAB il faut s'en passer.

APL offre la possibilité de numéroter (indicer) les composantes d'un vecteur à partir de zéro ou un. La variable primitive  (index origin) désigne cette origine ; on peut la choisir par  ou . Dans la pratique, l'origine zéro simplifie la programmation plus souvent que l'origine un.

Un algorithme simple

 

Le but de cet exemple est de comparer les deux versions d'une fonction qui utilise la même méthode pour calculer des nombres bien connus. Partons de la définition suivante : un nombre premier est un entier naturel dont le nombre de diviseurs est égal à 2. L'entier n>0 étant donné, il faut calculer la liste des nombres premiers  en programmant cette définition. Voici les deux fonctions :

Pour être raisonnable limitons-nous à 500 :

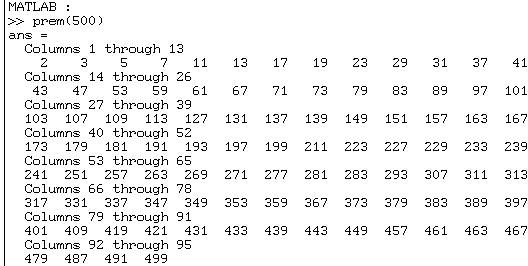
La fonction "Prem" est plus longue en MATLAB qu'en APL ; MATLAB encombre sa réponse de commentaires inutiles.

La liste des valeurs différentes dans un tableau

 

Voici une fonction qui donne la liste des valeurs différentes contenues dans un tableau dans l'ordre où elles s'y trouvent.

   

Exemple :

   

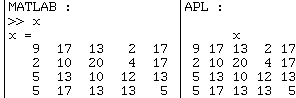
Les données étant rangées dans un ordre différent dans les deux langages, il faut transposer l'argument d'un côté ou de l'autre pour retrouver les résultats dans le même ordre :

   

La transposition s'écrit  en APL : elle fait tourner  la matrice autour de sa diagonale 

La fonction "ValDif" est plus longue en MATLAB qu'en APL.

Huit dames sur un échiquier

 

Il s'agit de disposer sur un échiquier huit dames mutuellement imprenables. Rappelons que l'échiquier est une table carrée de  cases ; il faut y placer huit dames (pièces du jeu) de manière qu'il y ait une dame sur chaque ligne, une dame sur chaque colonne, au plus une dame sur chaque parallèle aux deux diagonales ("\" et "/").

La fonction "dame" en MATLAB donne toutes les solutions sous la forme d'une matrice dont chaque colonne décrit une solution en indiquant, pour chaque ligne de l'échiquier, le numéro de la case que la dame doit y occuper. La fonction "Dame" en APL donne la même chose sous la forme transposée de la précédente, les cases étant numérotées à partir de zéro au lieu de un. Le côté de l'échiquier n'a pas d'importance pour l'algorithme ; on peut choisir une autre valeur que 8, c'est l'argument "n". Voici les deux fonctions :

Pour faciliter la comparaison des deux résultats, on ajoute 1 à la solution APL et on la transpose. Exemple pour la dimension 5 :

   

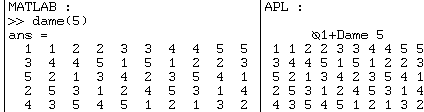
Une fonction "Visu" permet de visualiser ces solutions :

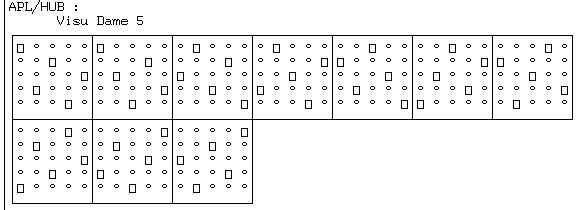
Parmi les solutions qui ne diffèrent entre elles que par une symétrie du carré, une fonction "NonSym" n'en retient qu'une :

     

La fonction "Dame" est plus longue en MATLAB qu'en APL.

La dimension des tableaux

 

En MATLAB les données sont des tableaux (arrays) dont la dimension comporte au moins deux nombres ; ce sont au moins des matrices. Un vecteur est une matrice ou bien à une ligne, ou bien à une colonne. Un scalaire est une matrice à une ligne et une colonne. La dimension peut comporter plus de deux nombres ; MATLAB parle alors de matrice multidimensionnelle.

En APL c'est la même chose, sauf que la dimension comporte un nombre pour un vecteur et zéro nombre pour un scalaire.

MATLAB parcourt les tableaux en faisant varier les premiers indices plus vite que les derniers (comme le fortran) : il écrit verticalement puis, quand la colonne est pleine, passe à la colonne suivante.

APL fait l'inverse : il écrit horizontalement puis, quand la ligne est pleine, passe à la ligne suivante, comme dans un texte français (ou anglais,...) normal.

Un tableau de dimension "3 4 5 6" est vu par MATLAB comme 6 paquets de 5 matrices de 4 colonnes de 3 cases, par APL comme 3 paquets de 4 matrices de 5 lignes de 6 cases. Pour visualiser le même tableau de la même façon, il faut le transformer par une des deux fonctions :

   

En MATLAB "visapl" simule comment APL présente un tableau ; en APL "VisMtl" simule comment MATLAB présente un tableau. Elles sont en quelque sorte inverses l'une de l'autre. Dans les exemples "Dim" construit en APL un tableau suivant les conventions de MATLAB.

Matrice de dimension "3 5" :

   

Notons qu'APL redimensionne 99 valeurs en ne prenant que les 15 premières valeurs.

Tableau de dimension "3 5 2" :

   

   

Tableau de dimension "3 5 3 2" :

   

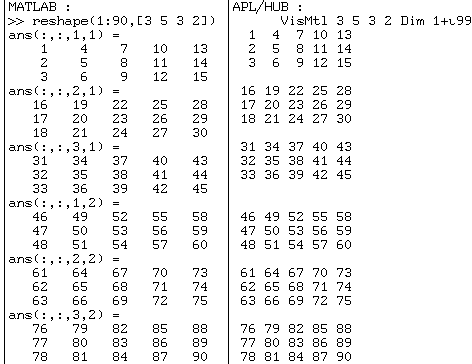
Dans MATLAB on trouve les fonctions "size", "reshape" (pourquoi pas resize ?), "zeros", "ones". En s'y prenant autrement, une seule fonction "dim" aurait pu faire tout cela, et même un peu plus : c'est ce que la primitive "ρ" (rho) fait en APL. On peut programmer "dim" en MATLAB ; la voici accompagnée de la fonction "Dim" qui simule la même chose en APL en tenant compte de la convention de rangement des valeurs par MATLAB :

   

Quand on travaille en APL, on n'a pas besoin de "Dim" puisque avec son arrangement des données la primitive "ρ" suffit :

   

Quand on l'appelle avec un argument, "dim" donne sa dimension, c'est ce que "size" fait. Considérons :

alors :

   

Changeons la dimension de "a" :

   

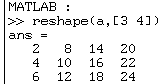
mais :

   

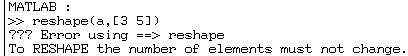
"reshape" exige que l'argument "a" contienne le même nombre de valeurs que le résultat.

Quand on l'appelle avec deux arguments, "dim" construit une matrice dont la dimension est décrite par le deuxième argument, en prenant cycliquement ses valeurs dans le premier argument ; "dim" n'exige pas que l'argument "a" contienne le même nombre de valeurs que le résultat. Pour faire la même chose il faut dans un langage ou dans l'autre retourner la dimension et transposer l'argument et le résultat, ce que la fonction "Dim" fait :

   

ou bien :

   

ou bien :

   

ou encore :

   

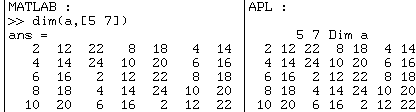
Avec "dim", les fonctions "zeros" et "ones" deviennent superflues :

   

   

   

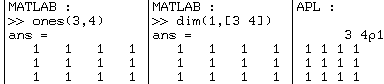
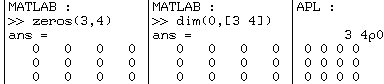
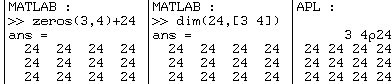
Ces exemples montrent qu'une fonction MATLAB bien conçue aurait pu en remplacer plusieurs pour faire la même chose avec moins de limitation.

Le produit des polynômes

 

Dans MATLAB il existe une fonction "conv" qui multiple deux polynômes. Pourquoi "conv" ? Parce que le produit de deux polynômes se ramène à un produit de convolution. Par souci de pédagogie, je préfère dire l'inverse. En APL/HUB c'est "PolMul". Mais "conv" ne multiplie que deux polynômes ; au-delà il faut itérer l'opération :

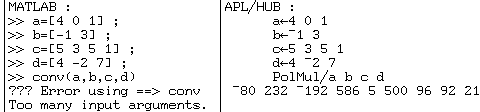
Il faut donc écrire :

ou programmer une boucle :

   

mais l'argument de "prodpoly" doit être un vecteur de cellules.

Cet exemple révèle l'impossibilité en MATLAB de répéter simplement une opération "conv" sur plusieurs données "a b c d". En APL la fonction "prodpoly" est superflue car la primitive "/" distribue la fonction "PolMul" entre les cases du vecteur gigogne "a" sans avoir rien à programmer.

Et la somme des polynômes ?

 

En MATLAB il faut programmer une fonction, par exemple ;

     

Le choix par MATLAB de ranger les coefficients suivant les puissances décroissantes est maladroit. Afin de placer les coefficients de la même puissance sur la même colonne la fonction "sompoly" range les coefficients de chaque polynôme suivant les puissances croissantes par "fliplr", puis, en fin de calcul, range les coefficients de la somme suivant les puissances décroissantes par "fliplr" pour que le résultat respecte la convention de MATLAB, comme les cases de l'argument. Notons aussi que "sum" fait la somme des lignes d'une matrice, sauf si elle ne contient qu'une ligne auquel cas elle fait la somme des colonnes ; c'est pour contourner cette exception gênante que "sompoly" initialise la copie des polynômes à deux lignes nulles.

En APL, où on range les coefficients suivant les puissances croissantes, on peut construire facilement l'instruction qui calcule la somme, "DISP" étant une fonction APL/HUB qui visualise la structure d'un tableau :

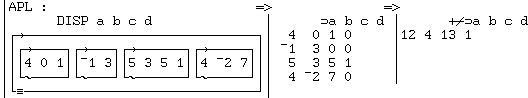
Pour ajouter ou multiplier un nombre quelconque de polynômes en MATLAB il a fallu programmer deux fonctions ; en APL il n'y a rien à programmer, quelques caractères suffisent.

Le produit matriciel dans les tableaux

 

En MATLAB on peut calculer le produit de deux matrices par la notation "a*b". Mais cela ne s'étend pas à des tableaux de plus de deux dimensions.

En APL ce produit s'écrit  et fonctionne sur des tableaux de dimensions quelconques. Par exemple si "a" a 3 dimensions et "b" en a 4, on aura :

  

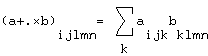
Voici une fonction "tabprod" qui, en MATLAB, fait la même chose que la combinaison de primitives  d'APL :

   

Par exemple, considérons un premier argument :

   

puis un deuxième argument :

   

et calculons le produit défini comme en APL :

   

Comparons les résultats :

   

Si le produit de matrices s'écrit  en APL, c'est parce que chaque valeur du résultat est une somme  de produits . C'est un cas particulier d'un concept général : celui de "f.g" où "f" et "g" sont deux fonctions quelconques calculant sur deux scalaires. Par exemple la combinaison  calcule des produits  de puissances  ; si on veut calculer :

on peut construire la matrice des exposants :

   

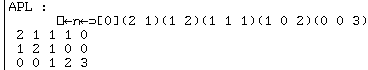
placer dans les variables "x" et "a" les valeurs

            

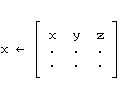
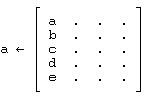
et l'expression

   

calcule alors "p".

De nombreuses fonctions mathématiques de MATLAB sont restreintes aux seules matrices.

La structure des données

 

En MATLAB les données sont des tableaux (arrays) dont la dimension comporte au moins deux nombres ; ce sont au moins des matrices. Un vecteur est une matrice, ou bien à une ligne, ou bien à une colonne. Un scalaire est une matrice à une ligne et une colonne. La dimension peut comporter plus de deux nombres ; MATLAB parle alors de matrice multidimensionnelle. Toutes les cases d'un même tableau doivent être de même type : logique, nombre, caractère, structure ou cellule (tableau) et ce type ne change que si on réaffecte le tableau tout entier. Si on affecte dans un tableau des valeurs de type différent, MATLAB convertit cette valeur s'il sait le faire, c'est-à-dire entre logique, nombre et caractère. Si les cases d'un tableau contiennent des caractères on peut y faire des opérations mathématiques : ajouter 10 aux caractères ! les multiplier par 3 ! les diviser par 2 ! etc... Si les cases d'un tableau contiennent des cellules ou des structures les opérations mathématiques sont interdites au tableau entier ; pour cela il faut sortir du tableau le contenu de chaque case pour faire le calcul.

En APL les données sont aussi des tableaux, mais la dimension comporte un seul nombre pour un vecteur et zéro nombre pour un scalaire, et aussi deux nombres pour une matrice, trois nombres pour un paquet de matrices, etc... Chaque case peut contenir, indépendamment des autres cases, un nombre, ou un caractère, ou un tableau ; dans ce dernier cas il s'agit d'un tableau gigogne ; ainsi les cases d'un même tableau peuvent être de types différents. Si on affecte dans un tableau des valeurs de type différent, aucune conversion n'intervient. Il n'y a donc qu'une seule structure de donnée, qui permet de faire tout ce qui nécessite des structures différentes en MATLAB. Toutes les fonctions primitives d'APL s'appliquent à ces tableaux, à tous les niveaux, sous réserve de compatibilité de dimension, logique, mathématique (on ne peut pas ajouter 10 à des caractères...), etc...

Exemple de conversion de caractères en nombres :

   

Exemple de conversion de nombres en caractères :

   

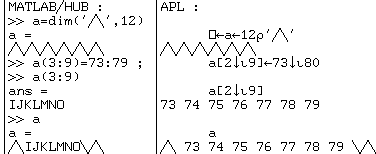
Exemples d'interdiction ; soit une variable :

   

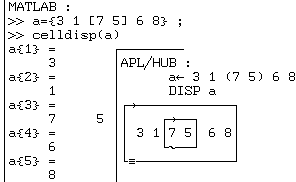
elle ne contient que des nombres auxquels MATLAB ne peut pas ajouter 10 :

   

Soit une autre variable :

   

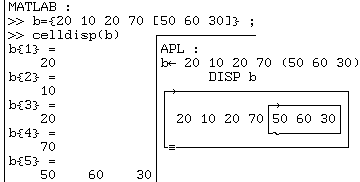
Ces deux variables ne contiennent que des nombres, mais MATLAB ne peut pas les ajouter :

tandis qu'APL sait faire tout cela.

L'utilisation convenable de cette propriété des données APL dans la programmation de la fonction "PolMul" permet la répercussion d'une valeur multiple sur le produit des polynômes :

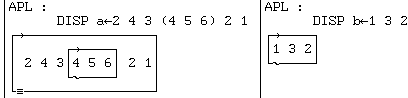
c'est-à-dire :

  

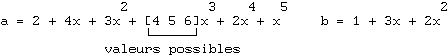
d'où le produit :

   

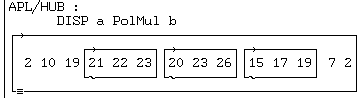
Ce travail est plus lourd en MATLAB, puisqu'il faut créer trois polynômes "a" et les multiplier par "b" un par un dans une boucle de programme.

L'unique structure des données APL est plus puissante et plus facile à manier que les diverses structures de données MATLAB.

Un polynôme et ses racines

 

MATLAB décrit un polynôme suivant les puissances décroissantes ; alors :

    "poly" construit un polynôme dont on donne les racines,

    "roots" calcule les racines d'un polynôme.

Construisons ainsi un polynôme de degré 6 :

   

puis calculons ses racines :

   

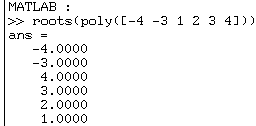
APL/HUB décrit un polynôme suivant les puissances croissantes : ainsi l'indice, en origine zéro, de chaque coefficient est égal à l'exposant de la variable pour le terme correspondant. Quand des nombres complexes sont susceptibles d'intervenir on les représente par leurs deux composantes ; on représente les vecteurs réels soit par une colonne (partie réelle), soit par deux, la deuxième (partie imaginaire) étant nulle. "PolRac" calcule un Polynôme (ou plusieurs) dont on donne les Racines : "RacPol" calcule les Racines d'un Polynôme (ou plusieurs). On obtient alors :

Jusqu'ici tout va bien.

En MATLAB "ones" construit une matrice pleine de "1" ; faisons le même exercice pour un polynôme dont les 6 racines valent 1 :

   

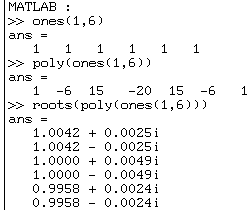
tandis que :

   

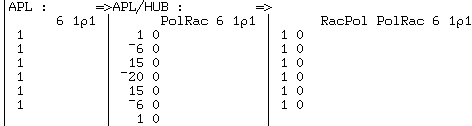
L'algorithme de MATLAB s'en tire bien quand c'est facile, les choses se gâtent quand c'est difficile ; celui d'APL/HUB calcule juste dans tous les cas.

Considérons maintenant le tableau à trois dimensions "p" qui contient deux polynômes et exécutons :

   

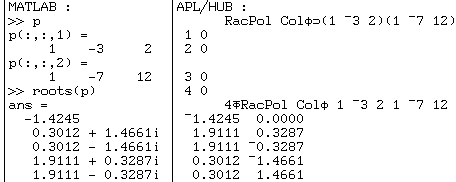
Au lieu de calculer les racines des deux polynômes :

        et   

il met bout à bout leurs coefficients, sans broncher, et calcule les racines du polynôme ainsi obtenu :

   

comme le prouve le calcul en APL/HUB. Absurde !

MATLAB ne prend pas assez de précautions pour garantir la précision de certains calculs ; il peut faire des calculs qui n'ont aucun sens.

Fonctions de MATLAB superflues en APL

 

Il existe dans MATLAB de nombreuses fonctions primitives dont APL se passe sans inconvénient.

D'abord APL a choisi d'abandonner les conventions d'écriture mathématique. C'est une habitude qu'on prend assez vite.

Toutes les fonctions ont la même syntaxe. Il y a trois types de fonctions : à zéro, un ou deux arguments. Par exemple si "F0" n'a pas d'argument, "F1" en a un "x" et "F2" en a deux "x" et "y", on les appelle par les expressions :

   

On a la correspondance :

   

et ici la fonction "F1" en APL a un argument droit subdivisé en trois sous-arguments "a", "b", "c". Dans l'expression :

   

la fonction "F2" a deux sous-arguments gauches "a", "b" et trois sous-arguments droits "c", "d", "e" ; il n'y a pas de correspondance en MATLAB où il faut se débrouiller autrement. Tout comme le signe de multiplication  se place entre deux nombres, la fonction "PolMul" se place entre deux polynômes :

   

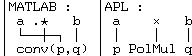
En APL la syntaxe est la même ; en MATLAB quand on passe des nombres aux polynômes, il faut changer de syntaxe.

Ensuite APL a abandonné toute priorité d'exécution, comme multiplication avant addition ; seule subsiste la priorité des parenthèses. Pour diverses raisons, une instruction ou l'intérieur d'une parenthèse s'exécutent de droite à gauche :

   

Si MATLAB, fortran, C... exécutaient vraiment de gauche à droite, on n'écrirait pas

   s = a*x + b*y + c*z

mais

   a*x + b*y + c*z = s

comme avec une calculette.

Puis APL dispose de primitives, appelées opérateurs, qui prennent une ou plusieurs fonctions comme arguments. Ainsi la réduction  répète sa fonction de gauche entre les colonnes (suivant la dernière dimension) de son argument droit ; nous avons vu cela dans :

   

La réduction  fait la même chose suivant la première dimension. Exemples de fonctions MATLAB superflues en APL :

   

et :

        

Le balayage  ou  permet par exemple :

   

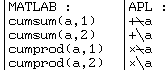
De nombreuses fonctions de MATLAB sont superflues en APL ; celui-ci les remplace par des combinaisons simples de primitives qui indiquent clairement ce qu'elles font.

Fonctions primitives APL absentes de MATLAB

 

Il existe dans APL des fonctions sans équivalent dans MATLAB. Il y a d'abord les fonctions qui travaillent sur les tableaux gigognes. Nous en avons vu un exemple à propos de la somme des polynômes ; la primitive  ouvre les cases d'un tableau, transformant un vecteur en matrice :

   

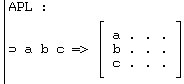
Voyons une autre primitive APL sans équivalent dans MATLAB.

La primitive  (iota) donne la première occurence d'une valeur dans un vecteur :

   

Ici "a" est un vecteur de dimension 12 et l'instruction  sert à adopter l'origine 1 pour les indices, comme en MATLAB. 16 de x est à la 7ème position dans a, 13 est pour la première fois à la 4ème, 22 à la 12ème,... 7 à la 13ème (au delà de "a") ...

Cette primitive  fonctionne avec des vecteurs gigognes :

   

Les fonctions de l'automatique

 

La "Control System Toolbox" contient des fonctions spécialisées à l'automatique. Pour se conformer à une certaine conception en vogue dans ce domaine, chaque case d'un tableau peut contenir une fraction rationnelle ; mais MATLAB l'appelle "fonction de transfert" (transfert function). On peut appeler la variable "s" ou "p" ou "z", mais pas "x" par exemple.

Transformée inverse de Laplace (automatique)

 

Pour calculer la transformée inverse de Laplace d'une fraction rationnelle F(p), il faut faire un détour : traiter F(p) comme la fonction de transfert d'un système linéaire invariant et lui appliquer une impulsion de Dirac. Prenons les deux fractions :

            

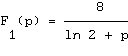
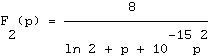
La valeur  est susceptible d'être cachée dans une description compliquée. La transformée inverse de F1(p) est exactement :

   

Notons  et  les pôles de F2(p), on a avec une bonne précision :

            

sa transformée inverse est :

   

Pour  le terme  est négligeable,  est très proche de ln 2 ; f2(t) est donc très proche de f1(t). Par le choix du coefficient ln 2 on voit que :

Nous ajoutons un terme du second degré nul au dénominateur de F1 pour ramener cette fraction à la même forme que F2.

En MATLAB on fait les deux calculs séparément :

   

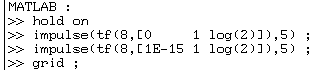
et cela donne :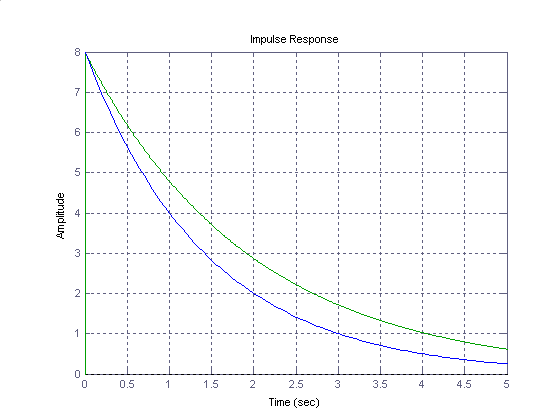

La courbe bleue de f1(t) est correcte ; mais la courbe verte montre que le coefficient 1E‑15 entraîne une dégradation appréciable de la précision de f2(t).

On peut encore construire un tableau "F" contenant les deux fractions précédentes et calculer f1(t) seule, puis f1(t) et f2(t) ensemble. On peut ensuite tracer f1(t) seule, puis extraite du calcul couplé avec f2(t) :

   

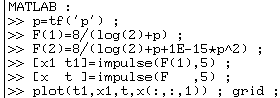
et cela donne :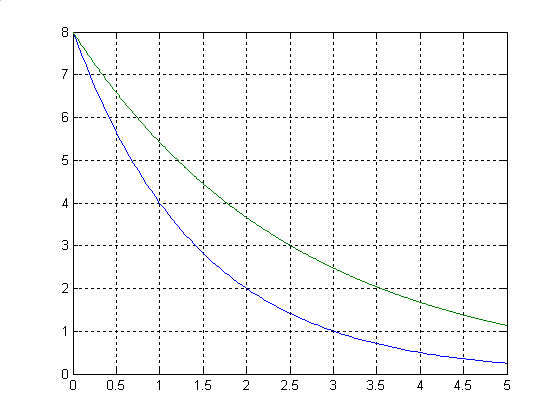

La courbe bleue de f1(t) calculée seule est correcte ; mais la courbe verte montre que la présence de f2(t) dans le calcul dégrade la précision de f1(t). Ici  n'est pas négligeable, cette petite cause produit de grands effets.

En APL/HUB on fait les deux calculs simultanément :

   

une ligne de code suffit, et cela donne :

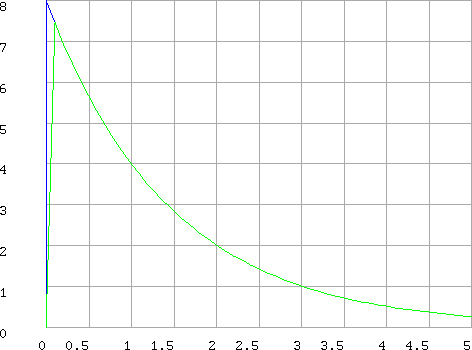
Puisque l'intervalle 5 est subdivisé en 50 parties, il y a un point à chaque multiple de 5/50=0.1 ; pour  la courbe f2(t) se superpose à f1(t) et l'écrase. Le coefficient 1E‑15 ne dégrade pas la précision. Le calcul proprement dit s'analyse :

   

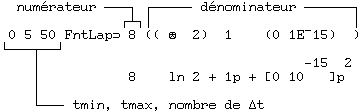
L'argument droit de "FntLap" est un tableau gigogne qui se développe :

   

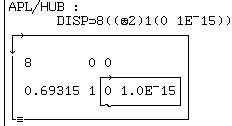
c'est une matrice à deux lignes (numérateur, dénominateur) et trois colonnes (second degré).

Au lieu de deux valeurs d'un coefficient on aurait pu en placer dix, cent, mille ; "FntLap" ferait encore les calculs simultanément, tandis qu'en MATLAB il faudrait faire une boucle de programme.

MATLAB ne prend pas assez de précautions pour garantir la précision de certains calculs.

Le temps de calcul (automatique)

 

Considérons un système d'ordre deux de fonction de transfert :

   

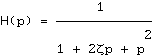
On veut tracer sa réponse à un échelon unité en fonction du coefficient d'amortissement  La transformée de Laplace de cette réponse est :

   

Prenons 100 valeurs de  en progression arithmétique :

    0.2, 0.4, ... 2

En APL on peut faire :

   

et sur un certain ordinateur on obtient après une seconde deux (1.2s) :

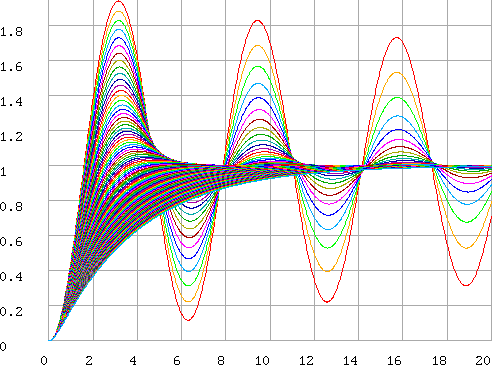
En MATLAB, par manque de tableaux gigognes analogues à APL, une manière facile consiste à faire une boucle dans une fonction ; chaque passage dans la boucle fait le calcul pour un  et trace la courbe correspondante :

   

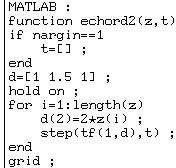
Puis on fait :

   

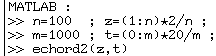
On obtient les mêmes courbes qu'avec APL sur le même ordinateur après soixante‑quinze secondes (75s).

Un utilisateur expérimenté de MATLAB a modifié la fonction "echord2" en déplaçant les courbes en dehors de la boucle :

   

On obtient encore les mêmes courbes sur le même ordinateur après une seconde deux (1.2s) aussi ; un piège.

En APL/HUB, c'est une seule ligne de code sans fonction. En APL/HUB, on peut se mettre dans les mêmes conditions que l'exemple MATLAB qui prend 75s en faisant chaque calcul et chaque courbe dans une boucle, donc dans une fonction ; on obtient le même graphique après une seconde neuf (1.9s) seulement.

Courbe de Black (automatique)

 

Dans l'étude d'un système asservi, on peut être amené à tracer sa fonction de transfert en boucle ouverte dans le plan de Black, appelé Nichols par MATLAB. Prenons comme exemple la fonction de transfert en boucle ouverte :

      

ce système est instable à cause d'un pôle à partie réelle positive. On trace la courbe de Black par :

   

ce qui donne :

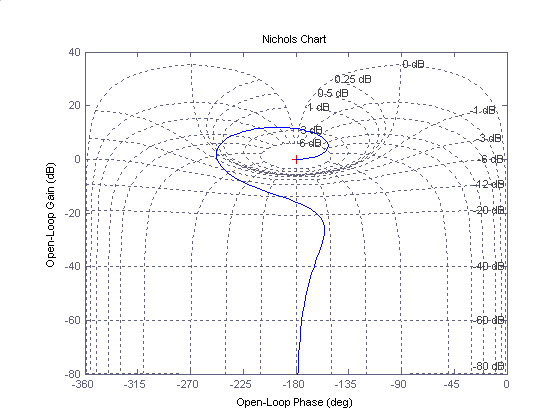
Si on multiplie F(p) par un coefficient de gain "K", ce qui translate verticalement la courbe de log K par rapport aux axes, on ne peut pas facilement en déduire le nombre de pôles instables (à parties réelles positives) en boucle fermée en fonction de K. De plus, la courbe est assortie d'une grille en traits interrompus qui permettait autrefois de calculer graphiquement, point par point, la fonction de transfert en boucle fermée. Depuis que l'ordinateur permet de faire ce calcul rapidement, cette grille est obsolète.

Une amélioration de la courbe de Black consiste à tracer le logarithme (complexe) de la courbe de Nyquist complète par :

où on a marqué quatre valeurs de K ; l'argument gauche de "BodBlk" s'analyse :

   

et cela donne :

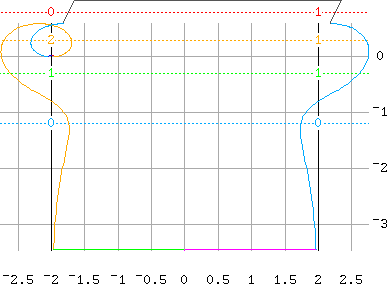
Le nombre de pôles instables (à parties réelles positives) en boucle fermée est le nombre de tours de la courbe autour des points critiques pour le réglage du gain ; il est indiqué sur la figure :

   

et on peut vérifier les pôles en boucle fermée arrondis à  près, encore une seule ligne de code pour calculer ces quatre cas :

L'argument droit de "LieuTrsf" se développe :

   

c'est une matrice à deux lignes : numérateur, dénominateur.

Le "nichols" de MATLAB ne trace que la partie jaune de "BodBlk" d'APL/HUB ; c'est la programmation moderne d'une technique obsolète.

Historique

 

J'ai abandonné le fortran en 1972 pour essayer puis adopter l'APL. Il y avait une différence colossale entre les deux langages. Beaucoup de gens étaient adversaires de l'APL, la majorité des informaticiens. Depuis cette époque, beaucoup d'informaticiens semblent manifester une farouche hostilité à l'APL. Pourquoi ? Diverses explications sont possibles, mais ce ne sont que des hypothèses.

La programmation en APL bouleversait les méthodes de l'informatique de l'époque. Par exemple, il ne fallait plus parcourir les cases d'un tableau pour les traiter une par une dans des boucles emboîtées, car APL fournissait des primitives efficaces sur tableaux. Les informaticiens n'y retrouvaient pas ce qu'ils avaient appris à l'école et, la programmation étant simplifiée, ils pouvaient craindre que des clients potentiels n'aient plus besoin de leurs services.

Les fonctions APL n'étaient pas compilées, mais interprétées ; et une règle disait que les programmes compilés s'exécutent plus vite que ceux interprétés. Ce n'était pas vrai pour toutes les fonctions APL, et on oubliait le temps passé par l'homme à l'analyse et à la programmation. Comparés à ceux d'aujourd'hui, les ordinateurs de l'époque (grosses armoires en salles climatisées) étaient lents et coûteux. Depuis, les méthodes d'interprétation se sont améliorées. Le travail en APL était globalement efficace, et ceux qui l'utilisaient couramment refusaient de revenir au fortran. Comme conséquence de cette hostilité, quand les décideurs d'une entreprise doivent acheter un logiciel, ils demandent conseil à leurs informaticiens qui ne leur recommandent surtout pas APL.

Vers 1990 on commence à entendre parler de MATLAB. Je me demande bien pourquoi ceux qui l'ont créé ont voulu refaire ce qui existait déjà en plus puissant, si ce n'est l'hostilité déjà signalée ; car APL connaissait les tableaux gigognes et un ensemble de concepts et de primitives permettant de les traiter efficacement par des programmes concis.

Bien entendu il existe des algorithmes d'analyse numérique en fortran, C ou MATLAB. Il en existe aussi en APL, nous en avons vu dans ce texte. Pour ceux qui n'existent pas en APL, il faut savoir que les diverses réalisations d'APL fournissent des passerelles entre APL et des algorithmes en binaire exécutable, qu'ils proviennent de fortran, C ou assembleur. De plus il faut comprendre qu'on peut traduire en APL des programmes fortran, C ou MATLAB sans trop de difficulté, car la version APL est toujours beaucoup plus simple. Naturellement cela représente un peu de travail ; mais il en vaut le coût. Ce faisant, on peut étendre le domaine d'application des algorithmes APL ainsi construits au-delà de ce qu'on peut espérer en fortran, C ou MATLAB. C'est la transformation inverse qui est compliquée, voire impossible.

Conclusion

 

MATLAB semble dériver du fortran, dont il a supprimé les déclarations de type et de dimension, auquel il a incorporé des matrices obligées.

Il essaie de forcer les données à être matricielles : par exemple il place les coefficients d'un polynôme dans une matrice à une ligne, alors que la notion de matrice n'a rien à voir avec celle de polynôme. Il fournit un grand nombre d'algorithmes de traitement réservé aux matrices. Mais si un problème ne peut pas être mis sous cette forme (arborescences, valeurs multiples d'une donnée, etc...) il faut faire une programmation du genre fortran.

Il y a des pièges dans fortran, il y en a aussi dans MATLAB mais ce ne sont toujours pas les mêmes.

Il y a plusieurs structures de données en MATLAB ; en APL une seule structure suffit pour en faire davantage.

Il y a plusieurs syntaxes en MATLAB suivant les fonctions ; en APL une seule syntaxe suffit, simplifiant la programmation.

Le choix des symboles de fonctions est plus restreint en MATLAB qu'en APL.

MATLAB place chaque fonction dans un fichier ; APL place toutes les fonctions en mémoire vive.

Les variables et fonctions d'APL s'organisent dans une structure arborescente dynamique ; dans MATLAB il n'y a que deux niveaux : privé et public.

Les fonctions qui font la même chose sont plus longues en MATLAB qu'en APL, quelquefois de beaucoup.

Une fonction MATLAB programmée en imitant APL peut en remplacer plusieurs tout en étant plus tolérante.

APL sait faire sans programmation des opérations que MATLAB ne peut faire qu'avec de longues fonctions.

Certains calculs numériques de MATLAB peuvent être faux, le choix de la méthode n'étant probablement pas le bon.

Certains calculs peuvent prendre plus de temps en MATLAB qu'en APL.

MATLAB peut faire des calculs qui n'ont aucun sens.

Certaines primitives de MATLAB sont superflues en APL.

Certaines primitives d'APL n'ont pas d'équivalent dans MATLAB.

......

Arrêtons là l'énumération ; bref, APL est plus simple, plus concis, plus puissant, plus cohérent et plus précis que MATLAB.

Pour ces raisons, et bien d'autres, je continue à utiliser APL et non pas MATLAB, qui compliquerait mon travail.

Le site :

    http://www.afapl.asso.fr

contient des fonctions APL, des articles sur APL, ainsi qu'une présentation d'APL.